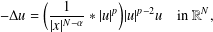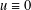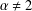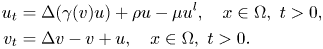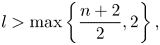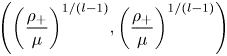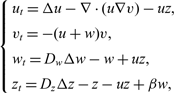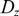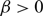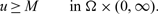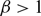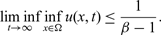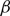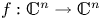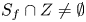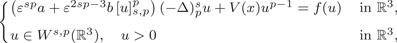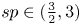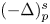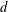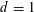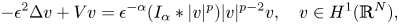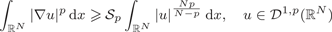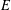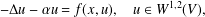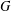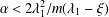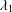Refine listing
Actions for selected content:
593 results in 35-XX
STABLE SOLUTIONS TO THE STATIC CHOQUARD EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 10 June 2020, pp. 471-478
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
An n-dimensional chemotaxis system with signal-dependent motility and generalized logistic source: global existence and asymptotic stabilization
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 29 May 2020, pp. 821-841
- Print publication:
- April 2021
-
- Article
- Export citation
A LIPSCHITZ METRIC FOR THE CAMASSA–HOLM EQUATION
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 21 May 2020, e27
-
- Article
-
- You have access
- Open access
- Export citation
Conditional symmetries and exact solutions of a nonlinear three-component reaction-diffusion model
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 11 May 2020, pp. 280-300
-
- Article
- Export citation
A critical virus production rate for efficiency of oncolytic virotherapy
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 08 May 2020, pp. 301-316
-
- Article
- Export citation
On topological approaches to the Jacobian conjecture in ℂn
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 07 May 2020, pp. 666-675
-
- Article
- Export citation
Concentration of positive solutions for a class of fractional p-Kirchhoff type equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 04 May 2020, pp. 601-651
- Print publication:
- April 2021
-
- Article
- Export citation
Edge corrections for parallel-plate capacitors
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 30 April 2020, pp. 226-241
-
- Article
-
- You have access
- Open access
- Export citation
Transition waves for lattice Fisher-KPP equations with time and space dependence
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 28 April 2020, pp. 573-600
- Print publication:
- April 2021
-
- Article
- Export citation
Relaxation of the Cahn–Hilliard equation with singular single-well potential and degenerate mobility
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 24 March 2020, pp. 89-112
-
- Article
- Export citation
A novel Landau-de Gennes model with quartic elastic terms
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 24 March 2020, pp. 177-198
-
- Article
- Export citation
Hopf bifurcation from spike solutions for the weak coupling Gierer–Meinhardt system
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 17 March 2020, pp. 113-145
-
- Article
- Export citation
FRACTIONAL SCHRÖDINGER–POISSON SYSTEM WITH SINGULARITY: EXISTENCE, UNIQUENESS, AND ASYMPTOTIC BEHAVIOR
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 12 March 2020, pp. 179-192
-
- Article
-
- You have access
- Export citation
On approximating minimizers of convex functionals with a convexity constraint by singular Abreu equations without uniform convexity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 11 March 2020, pp. 356-376
- Print publication:
- February 2021
-
- Article
- Export citation
LONG TIME BEHAVIOR OF THE SOLUTIONS OF NLW ON THE
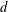 $d$-DIMENSIONAL TORUS
$d$-DIMENSIONAL TORUS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 06 March 2020, e12
-
- Article
-
- You have access
- Open access
- Export citation
Multiple bound states of higher topological type for semi-classical Choquard equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 04 March 2020, pp. 329-355
- Print publication:
- February 2021
-
- Article
- Export citation
Nondegeneracy of the bubble for the critical p-Laplace equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 151-168
- Print publication:
- February 2021
-
- Article
- Export citation
ON A CLASS OF NONLINEAR SCHRÖDINGER EQUATIONS ON FINITE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 477-487
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Nonlinear fractional Laplacian problems with nonlocal ‘gradient terms’
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 04 February 2020, pp. 2682-2718
- Print publication:
- October 2020
-
- Article
- Export citation
QUADRATIC DIFFERENTIAL EQUATIONS: PARTIAL GELFAND–SHILOV SMOOTHING EFFECT AND NULL-CONTROLLABILITY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 31 January 2020, pp. 1749-1801
- Print publication:
- November 2021
-
- Article
- Export citation