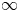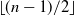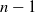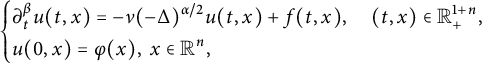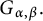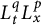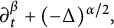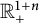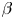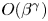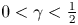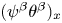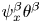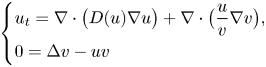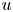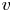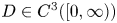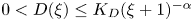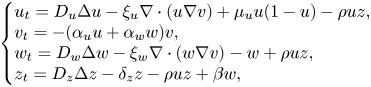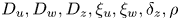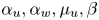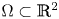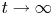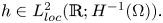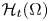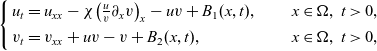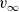Refine listing
Actions for selected content:
301 results in 35Kxx
The monostable cooperative system with nonlocal diffusion and free boundaries
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 20 March 2023, pp. 629-659
- Print publication:
- April 2024
-
- Article
- Export citation
Existence of weak solutions to an anisotropic parabolic–parabolic chemotaxis system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 06 March 2023, pp. 424-444
- Print publication:
- April 2024
-
- Article
- Export citation
Asymptotic profiles for positive solutions of diffusive logistic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 15 February 2023, pp. 273-284
- Print publication:
- February 2024
-
- Article
- Export citation
Exact nonclassical symmetry solutions of Lotka–Volterra-type population systems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 25 November 2022, pp. 998-1016
-
- Article
- Export citation
A deterministic gradient-based approach to avoid saddle points
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 09 November 2022, pp. 738-757
-
- Article
- Export citation
Application of capacities to space–time fractional dissipative equations I: regularity and the blow-up set
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 25 October 2022, pp. 1904-1956
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Homogenisation of a two-phase problem with nonlinear dynamic Wentzell-interface condition for connected–disconnected porous media
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 21 June 2022, pp. 617-641
-
- Article
- Export citation
Boundary layer of Hsieh's equation with conservative nonlinearity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 09 June 2022, pp. 1167-1197
- Print publication:
- August 2023
-
- Article
- Export citation
Finite-time blow-up in a repulsive chemotaxis-consumption system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 06 June 2022, pp. 1150-1166
- Print publication:
- August 2023
-
- Article
- Export citation
A NEW NONLOCAL NONLINEAR DIFFUSION EQUATION: THE ONE-DIMENSIONAL CASE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 05 May 2022, pp. 333-339
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic and transient dynamics of SEIR epidemic models on weighted networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 26 April 2022, pp. 238-261
-
- Article
- Export citation
Asymptotic behaviour in a doubly haptotactic cross-diffusion model for oncolytic virotherapy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 19 April 2022, pp. 881-906
- Print publication:
- June 2023
-
- Article
- Export citation
The stability analysis of a 2D Keller–Segel–Navier–Stokes system in fast signal diffusion
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 31 March 2022, pp. 160-209
-
- Article
-
- You have access
- HTML
- Export citation
Corrigendum: Dynamics of a susceptible—infected—susceptible epidemic reaction—diffusion model
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 30 March 2022, pp. 718-720
- Print publication:
- April 2023
-
- Article
-
- You have access
- HTML
- Export citation
Existence and uniqueness of solutions to a flow and transport problem with degenerating coefficients
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 03 February 2022, pp. 55-76
-
- Article
-
- You have access
- HTML
- Export citation
Spreading speeds and traveling wave solutions of diffusive vector-borne disease models without monotonicity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 13 December 2021, pp. 137-166
- Print publication:
- February 2023
-
- Article
- Export citation
Existence and regularity of time-dependent pullback attractors for the non-autonomous nonclassical diffusion equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 18 November 2021, pp. 1533-1550
- Print publication:
- December 2022
-
- Article
- Export citation
On the global existence and qualitative behaviour of one-dimensional solutions to a model for urban crime
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 02 November 2021, pp. 919-959
-
- Article
- Export citation
BOUNDS ON THE CRITICAL TIMES FOR THE GENERAL FISHER–KPP EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 63 / Issue 4 / October 2021
- Published online by Cambridge University Press:
- 02 November 2021, pp. 448-468
-
- Article
- Export citation
On the initial value problem for a class of nonlinear biharmonic equation with time-fractional derivative
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 26 August 2021, pp. 989-1031
- Print publication:
- August 2022
-
- Article
- Export citation