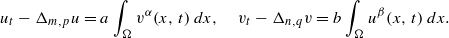Refine listing
Actions for selected content:
309 results in 35Kxx
Existence and blow-up of solutions for a non-local filtration and porous medium problem
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 12 January 2010, pp. 195-209
-
- Article
-
- You have access
- Export citation
MODELLING SEA ICE GROWTH
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 3 / January 2009
- Published online by Cambridge University Press:
- 03 November 2009, pp. 306-319
-
- Article
-
- You have access
- Export citation
A CONLEY INDEX CALCULATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 13 August 2009, pp. 510-520
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
Critical extinction and blow-up exponents for fast diffusive polytropic filtration equation with sources
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 28 May 2009, pp. 419-444
-
- Article
-
- You have access
- Export citation
A note on an ill-posed problem for the heat equation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 32 / Issue 3 / June 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 358-368
-
- Article
-
- You have access
- Export citation
Growth of solutions of weakly coupled parabolic systems and Laplace's equation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 3 / December 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 391-403
-
- Article
-
- You have access
- Export citation
Time-isolated Singularities of Temperatures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 3 / December 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 416-429
-
- Article
-
- You have access
- Export citation
On mean curvature flow of spacelike hypersurfaces in asymptotically flat spacetimes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 1 / August 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 41-59
-
- Article
-
- You have access
- Export citation
Homogeneous solutions of the generalized heat equation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 1 / February 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 13-45
-
- Article
-
- You have access
- Export citation
Two estimates concerning asymptotics of the minimizations of a Ginzburg-Landau functional
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 1 / February 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 128-140
-
- Article
-
- You have access
- Export citation
An extension of the principle of spatial averaging for inertial manifolds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 1 / February 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 125-142
-
- Article
-
- You have access
- Export citation
Heat Kernels on homogeneous spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 1 / February 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 109-147
-
- Article
-
- You have access
- Export citation
Initial and relative limiting behaviour of temperatures on a strip
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 33 / Issue 2 / October 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 213-228
-
- Article
-
- You have access
- Export citation
Representation theorems for parabolic systems
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 32 / Issue 2 / April 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 246-288
-
- Article
-
- You have access
- Export citation
The persistence of logconcavity for positive solutions of the one dimensional heat equation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 2 / April 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 246-263
-
- Article
-
- You have access
- Export citation
The Appell transform and the semigroup property for temperatures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 1 / February 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 109-117
-
- Article
-
- You have access
- Export citation
Quasi-linear parabolic partial differential equations with delays in the highest order spatial derivatives
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 2 / April 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 174-203
-
- Article
-
- You have access
- Export citation
Second-order strongly elliptic operators on Lie groups with Hölder continuous coefficients
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 3 / December 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-363
-
- Article
-
- You have access
- Export citation
HEAT KERNEL BOUNDS, POINCARÉ SERIES, AND L2 SPECTRUM FOR LOCALLY SYMMETRIC SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 73-86
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
GLOBAL EXISTENCE AND BLOW-UP FOR A NON-NEWTON POLYTROPIC FILTRATION SYSTEM WITH NONLOCAL SOURCE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 13-29
-
- Article
-
- You have access
- Export citation
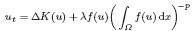
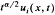 exceeds 1. Related results for Poisson integrals on a half-space are also described, some applications are given, and interesting comparisons emerge.
exceeds 1. Related results for Poisson integrals on a half-space are also described, some applications are given, and interesting comparisons emerge.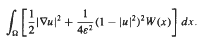 .
.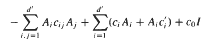 in divergence form corresponding to a quadratic form with complex coefficients, bounded Hölder continuous principal coefficients
in divergence form corresponding to a quadratic form with complex coefficients, bounded Hölder continuous principal coefficients 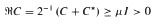 uniformly over
uniformly over 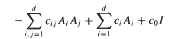 in non-divergence form for which the principal coefficients are at least once differentiable.
in non-divergence form for which the principal coefficients are at least once differentiable.