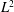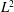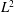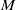Refine listing
Actions for selected content:
300 results in 35Kxx
QUASI RIESZ TRANSFORMS, HARDY SPACES AND GENERALISED SUB-GAUSSIAN HEAT KERNEL ESTIMATES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 10 August 2015, pp. 508-510
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
On the continuation of solutions of non-autonomous semilinear parabolic problems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 13 July 2015, pp. 17-55
-
- Article
- Export citation
OBSERVATIONS ON GAUSSIAN UPPER BOUNDS FOR NEUMANN HEAT KERNELS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 08 July 2015, pp. 429-439
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
On fractional heat equations with non-local initial conditions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 08 July 2015, pp. 65-76
-
- Article
- Export citation
A DIFFUSIVE LOGISTIC EQUATION WITH MEMORY IN BESSEL POTENTIAL SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 16 June 2015, pp. 251-258
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
ESTIMATES OF GREEN’S FUNCTION FOR SECOND-ORDER PARABOLIC EQUATIONS NEAR EDGES
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 17 April 2015, pp. 345-369
- Print publication:
- May 2015
-
- Article
- Export citation
THERMIC MINORANTS AND REDUCTIONS OF SUPERTEMPERATURES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 06 March 2015, pp. 128-144
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
MAXIMAL HARDY SPACES ASSOCIATED TO NONNEGATIVE SELF-ADJOINT OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 23 December 2014, pp. 286-302
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
Generalized Morrey Regularity for Parabolic Equations with Discontinuous Data
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 10 December 2014, pp. 199-218
-
- Article
-
- You have access
- Export citation
Numerical Approximation of Stationary Distributions for Stochastic Partial Differential Equations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 858-873
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
REGULARITY OF BOUNDARY POINTS IN THE DIRICHLET PROBLEM FOR THE HEAT EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 476-485
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
OPTIMAL
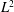 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L^2$ ESTIMATES FOR THE SEMIDISCRETE GALERKIN METHOD APPLIED TO PARABOLIC INTEGRO-DIFFERENTIAL EQUATIONS WITH NONSMOOTH DATA
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L^2$ ESTIMATES FOR THE SEMIDISCRETE GALERKIN METHOD APPLIED TO PARABOLIC INTEGRO-DIFFERENTIAL EQUATIONS WITH NONSMOOTH DATA
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 3 / January 2014
- Published online by Cambridge University Press:
- 05 June 2014, pp. 245-266
-
- Article
-
- You have access
- Export citation
VORTEX LIQUIDS AND THE GINZBURG–LANDAU EQUATION
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 27 May 2014, e11
-
- Article
-
- You have access
- Open access
- Export citation
A TRANSFORMATION METHOD FOR SOLVING THE HAMILTON–JACOBI–BELLMAN EQUATION FOR A CONSTRAINED DYNAMIC STOCHASTIC OPTIMAL ALLOCATION PROBLEM
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 1 / July 2013
- Published online by Cambridge University Press:
- 10 October 2013, pp. 14-38
-
- Article
-
- You have access
- Export citation
Poincaré–Lelong equation via the Hodge–Laplace heat equation
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 11 / November 2013
- Published online by Cambridge University Press:
- 09 September 2013, pp. 1856-1870
- Print publication:
- November 2013
-
- Article
- Export citation
AN IMPROVED SECOND-ORDER NUMERICAL METHOD FOR THE GENERALIZED BURGERS–FISHER EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 54 / Issue 3 / January 2013
- Published online by Cambridge University Press:
- 12 June 2013, pp. 181-199
-
- Article
-
- You have access
- Export citation
Averaging for a Fully Coupled Piecewise-Deterministic Markov Process in Infinite Dimensions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 749-773
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
CRITICAL CURVES FOR A COUPLED SYSTEM OF FAST DIFFUSIVE NEWTONIAN FILTRATION EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 07 June 2012, pp. 440-447
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
A COMPARISON OF CRITICAL TIME DEFINITIONS IN MULTILAYER DIFFUSION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 52 / Issue 4 / April 2011
- Published online by Cambridge University Press:
- 20 March 2012, pp. 333-358
-
- Article
-
- You have access
- Export citation
DOMAIN PERTURBATION FOR PARABOLIC EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 16 December 2011, pp. 174-176
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
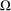
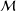
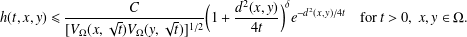
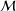
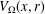
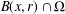
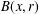


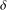
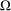
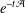
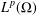
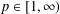

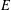

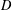
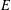


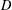
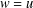
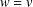
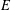
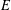
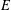
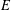
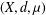
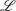
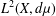
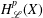
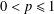
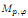 of sublinear operators generated by the parabolic Calderón—Zygmund operator and by the commutator of this operator with bounded mean oscillation (BMO) functions. As a consequence, we obtain a global
of sublinear operators generated by the parabolic Calderón—Zygmund operator and by the commutator of this operator with bounded mean oscillation (BMO) functions. As a consequence, we obtain a global