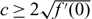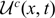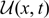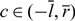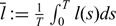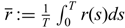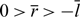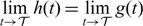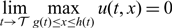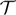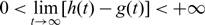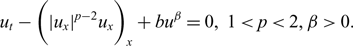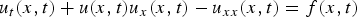Refine listing
Actions for selected content:
308 results in 35Kxx
Existence and uniqueness of monotone wavefronts in a nonlocal resource-limited model
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 07 May 2019, pp. 2462-2483
- Print publication:
- October 2020
-
- Article
- Export citation
Nonlinear systems coupled through multi-marginal transport problems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 April 2019, pp. 450-469
-
- Article
- Export citation
Global well-posedness of advective Lotka–Volterra competition systems with nonlinear diffusion
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 03 April 2019, pp. 2322-2348
- Print publication:
- October 2020
-
- Article
- Export citation
Entire solutions of the Fisher–KPP equation on the half line
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 26 March 2019, pp. 407-422
-
- Article
- Export citation
Pointwise stability of reaction diffusion fronts
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 2216-2254
- Print publication:
- October 2020
-
- Article
- Export citation
Asymptotic behaviour of solutions of Fisher–KPP equation with free boundaries in time-periodic environment
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 423-449
-
- Article
- Export citation
Evolution of interfaces for the nonlinear parabolic p-Laplacian-type reaction-diffusion equations. II. Fast diffusion vs. absorption
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 18 March 2019, pp. 385-406
-
- Article
- Export citation
On non-autonomously forced Burgers equation with periodic and Dirichlet boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 14 March 2019, pp. 2025-2054
- Print publication:
- August 2020
-
- Article
- Export citation
Wave propagation for a class of non-local dispersal non-cooperative systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 14 March 2019, pp. 1965-1997
- Print publication:
- August 2020
-
- Article
- Export citation
On a model for phase separation on biological membranes and its relation to the Ohta–Kawasaki equation
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 11 March 2019, pp. 297-338
-
- Article
- Export citation
A particle system approach to aggregation phenomena
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 12 July 2019, pp. 282-306
- Print publication:
- March 2019
-
- Article
- Export citation
EXTENDABLE TEMPERATURES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 27 February 2019, pp. 297-303
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Corrigendum to: Dirichlet and Neumann boundary conditions for the p-Laplace operator: What is in between?
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1689-1691
- Print publication:
- December 2019
-
- Article
- Export citation
Axisymmetric flows in the exterior of a cylinder
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1671-1698
- Print publication:
- August 2020
-
- Article
- Export citation
Linearized stability implies dynamic stability for equilibria of 1-dimensional, p-Laplacian boundary value problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1313-1338
- Print publication:
- June 2020
-
- Article
- Export citation
Monotonicity of non-Liouville property for positive solutions of skew product elliptic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1429-1449
- Print publication:
- June 2020
-
- Article
- Export citation
On higher differentiability of solutions of parabolic systems with discontinuous coefficients and (p, q)-growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 419-451
- Print publication:
- February 2020
-
- Article
- Export citation
Asymptotically self-similar behaviour of global solutions for semilinear heat equations with algebraically decaying initial data
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 789-811
- Print publication:
- April 2020
-
- Article
- Export citation
Existence of bistable waves for a nonlocal and nonmonotone reaction-diffusion equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 721-739
- Print publication:
- April 2020
-
- Article
- Export citation
Complete quenching phenomenon and instantaneous shrinking of support of solutions of degenerate parabolic equations with nonlinear singular absorption
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 17 January 2019, pp. 1323-1346
- Print publication:
- October 2019
-
- Article
- Export citation