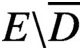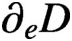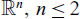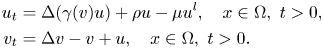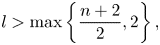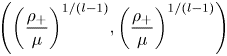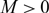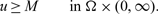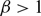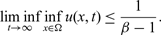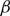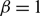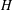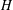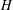Refine listing
Actions for selected content:
300 results in 35Kxx
UNIQUENESS OF EXTENDABLE TEMPERATURES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 02 October 2020, pp. 311-317
- Print publication:
- April 2021
-
- Article
- Export citation
A reaction–diffusion epidemic model with incubation period in almost periodic environments
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 25 September 2020, pp. 1153-1176
-
- Article
- Export citation
Coarse graining of a Fokker–Planck equation with excluded volume effects preserving the gradient flow structure
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 22 September 2020, pp. 711-745
-
- Article
-
- You have access
- Open access
- Export citation
Non-monotone waves of a stage-structured SLIRM epidemic model with latent period
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 15 September 2020, pp. 1407-1442
- Print publication:
- October 2021
-
- Article
- Export citation
Immediate smoothing and global solutions for initial data in L1 × W1,2 in a Keller–Segel system with logistic terms in 2D
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 02 September 2020, pp. 1204-1224
- Print publication:
- August 2021
-
- Article
- Export citation
Global dynamics and spatio-temporal patterns of predator–prey systems with density-dependent motion
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 12 August 2020, pp. 652-682
-
- Article
- Export citation
Some further results on the nonlocal p-Laplacian type problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 07 August 2020, pp. 953-970
- Print publication:
- June 2021
-
- Article
- Export citation
On decay rates of the solutions of parabolic Cauchy problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 21 July 2020, pp. 1021-1039
- Print publication:
- June 2021
-
- Article
- Export citation
Does indirectness of signal production reduce the explosion-supporting potential in chemotaxis–haptotaxis systems? Global classical solvability in a class of models for cancer invasion (and more)
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 17 July 2020, pp. 618-651
-
- Article
- Export citation
Global and exponential attractor of the repulsive Keller–Segel model with logarithmic sensitivity
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 30 June 2020, pp. 599-617
-
- Article
- Export citation
Approximate solutions to one-phase Stefan-like problems with space-dependent latent heat
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 15 June 2020, pp. 337-369
-
- Article
- Export citation
An n-dimensional chemotaxis system with signal-dependent motility and generalized logistic source: global existence and asymptotic stabilization
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 29 May 2020, pp. 821-841
- Print publication:
- April 2021
-
- Article
- Export citation
Conditional symmetries and exact solutions of a nonlinear three-component reaction-diffusion model
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 11 May 2020, pp. 280-300
-
- Article
- Export citation
A critical virus production rate for efficiency of oncolytic virotherapy
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 08 May 2020, pp. 301-316
-
- Article
- Export citation
DEFORMING A STARSHAPED CURVE INTO A CIRCLE BY AN AREA-PRESERVING FLOW
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 23 April 2020, pp. 498-505
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
AN UNCERTAINTY PRINCIPLE FOR SOLUTIONS OF THE SCHRÖDINGER EQUATION ON
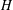 $H$-TYPE GROUPS
$H$-TYPE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 02 April 2020, pp. 1-16
- Print publication:
- August 2021
-
- Article
- Export citation
Existence results for the Kudryashov–Sinelshchikov–Olver equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 01 April 2020, pp. 425-450
- Print publication:
- April 2021
-
- Article
- Export citation
Existence and stability of bistable wavefronts in a nonlocal delayed reaction–diffusion epidemic system
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 24 March 2020, pp. 146-176
-
- Article
- Export citation
Well-posedness for nonlinear SPDEs with strongly continuous perturbation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 11 March 2020, pp. 265-295
- Print publication:
- February 2021
-
- Article
-
- You have access
- Open access
- Export citation
ANCIENT SOLUTIONS OF CODIMENSION TWO SURFACES WITH CURVATURE PINCHING - RETRACTED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 06 March 2020, pp. 162-171
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation