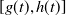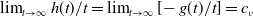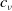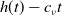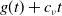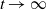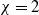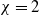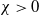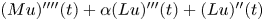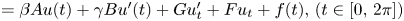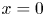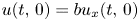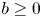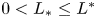Refine listing
Actions for selected content:
300 results in 35Kxx
Sharp asymptotic profile of the solution to a West Nile virus model with free boundary
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 13 October 2023, pp. 462-482
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The solvability for a nonlinear degenerate hyperbolic–parabolic coupled system arising from nematic liquid crystals
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 13 October 2023, pp. 1823-1890
- Print publication:
- December 2024
-
- Article
- Export citation
Long-time dynamics and semi-wave of a delayed nonlocal epidemic model with free boundaries
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 05 October 2023, pp. 564-610
- Print publication:
- April 2025
-
- Article
- Export citation
Generalised solution to a 2D parabolic-parabolic chemotaxis system for urban crime: Global existence and large-time behaviour
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 25 September 2023, pp. 409-429
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Steady-state solutions for a reaction–diffusion equation with Robin boundary conditions: Application to the control of dengue vectors
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 18 September 2023, pp. 382-408
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Periodic solutions of four-order degenerate differential equations with finite delay in vector-valued function spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 14 September 2023, pp. 395-412
- Print publication:
- April 2025
-
- Article
- Export citation
Asymptotic formulas of the eigenvalues for the linearization of the scalar field equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 11 September 2023, pp. 307-344
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete heat equation with irregular thermal conductivity and tempered distributional data
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 04 September 2023, pp. 57-80
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spreading dynamics of a diffusive epidemic model with free boundaries and two delays
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 11 August 2023, pp. 1133-1169
-
- Article
- Export citation
The effect of pore-scale contaminant distribution on the reactive decontamination of porous media
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 08 August 2023, pp. 318-358
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sliding methods for tempered fractional parabolic problem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 28 July 2023, pp. 1358-1378
- Print publication:
- August 2024
-
- Article
- Export citation
EXACT SOLUTIONS OF HYPERBOLIC REACTION-DIFFUSION EQUATIONS IN TWO DIMENSIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 4 / October 2022
- Published online by Cambridge University Press:
- 17 July 2023, pp. 338-354
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CURVATURE-TORSION ENTROPY FOR TWISTED CURVES UNDER CURVE SHORTENING FLOW
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 11 July 2023, pp. 571-580
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Interface behaviour of the slow diffusion equation with strong absorption: Intermediate-asymptotic properties
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 14 June 2023, pp. 1099-1132
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effect of the location of a protection zone in a reaction–diffusion model
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 14 June 2023, pp. 1095-1117
- Print publication:
- August 2024
-
- Article
- Export citation
Uniform bound on the number of partitions for optimal configurations of the Ohta–Kawasaki energy in 3D
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 May 2023, pp. 1341-1353
- Print publication:
- December 2023
-
- Article
- Export citation
General kernel estimates of Schrödinger-type operators with unbounded diffusion terms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 19 May 2023, pp. 929-960
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Extended symmetry analysis of remarkable (1+2)-dimensional Fokker–Planck equation
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 05 May 2023, pp. 1067-1098
-
- Article
- Export citation
Local regularity for nonlinear elliptic and parabolic equations with anisotropic weights
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 28 April 2023, pp. 391-436
-
- Article
- Export citation
The monostable cooperative system with nonlocal diffusion and free boundaries
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 20 March 2023, pp. 629-659
- Print publication:
- April 2024
-
- Article
- Export citation