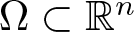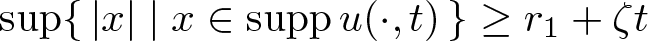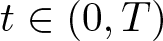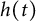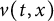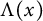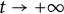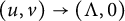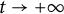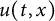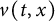Refine listing
Actions for selected content:
301 results in 35Kxx
Propagation dynamics of time-dependent reaction-diffusion equations under climate change in an infinite cylinder
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 19 December 2025, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a Cahn–Hilliard equation for the growth and division of chemically active droplets modelling protocells
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 06 November 2025, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Impact of birth pulse and environment shift on population survival and propagation
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 17 October 2025, pp. 1-27
-
- Article
- Export citation
A remark on the long-time asymptotics of global-in-time solutions for semilinear parabolic equations in
 ${\mathbb {R}^N}$
${\mathbb {R}^N}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 10 October 2025, pp. 1-21
-
- Article
- Export citation
Nonlinear Hodge flows in symplectic geometry
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 17 December 2025, pp. 2461-2492
- Print publication:
- October 2025
-
- Article
- Export citation
Shrinking vs. expanding: the evolution of spatial support in degenerate Keller–Segel systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 September 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Anisotropic area-preserving flows for plane curves and entropy inequalities
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 23 September 2025, pp. 1-25
-
- Article
- Export citation
Global dynamics of a degenerate reaction-diffusion cholera model with phage-bacteria interaction in a heterogeneous environment
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 22 September 2025, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the convergence of non-integer linear Hopf flow
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 12 September 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global existence and some qualitative properties of weak solutions for a class of pseudo-parabolic equations with a logarithmic nonlinearity in whole
 $\mathbb{R}^{N}$
$\mathbb{R}^{N}$
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 August 2025, pp. 1-44
-
- Article
- Export citation
On a Santaló point for Nakamura-Tsuji’s Laplace transform inequality
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 July 2025, e125
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Existence-uniqueness theory and small-data decay for a reaction-diffusion model of wildfire spread
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 08 July 2025, pp. 1347-1358
- Print publication:
- December 2025
-
- Article
- Export citation
A free boundary problem of competition-diffusion system with Dirichlet boundary condition
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 07 July 2025, pp. 1-20
-
- Article
- Export citation
Global boundedness and stabilization of solutions for a chemotaxis system with acceleration and logistic source
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-30
-
- Article
- Export citation
The evolution problem for the 1D nonlocal Fisher-KPP equation with a top hat kernel. Part 2. The initial-boundary value problem on a finite domain
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cahn–Hilliard equations with singular potential, reaction term and pure phase initial datum
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 27 May 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Collapsing immortal Kähler-Ricci flows
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 May 2025, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DELAYED HOPF BIFURCATIONS IN REACTION–DIFFUSION SYSTEMS IN TWO SPACE DIMENSIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 13 May 2025, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global dynamics for the generalised chemotaxis-Navier–Stokes system in
 $\mathbb{R}^3$
$\mathbb{R}^3$
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 22 April 2025, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pattern formation with jump discontinuity in a predator–prey model with Holling-II functional response
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1160-1182
-
- Article
-
- You have access
- Open access
- HTML
- Export citation