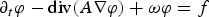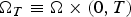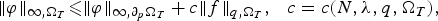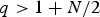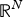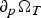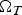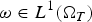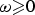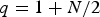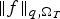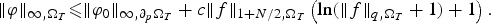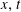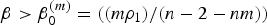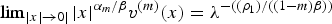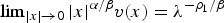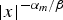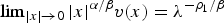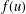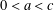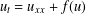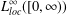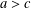Refine listing
Actions for selected content:
308 results in 35Kxx
Logarithmic upper bounds for weak solutions to a class of parabolic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1481-1491
- Print publication:
- December 2019
-
- Article
- Export citation
Existence of travelling waves with the critical speed for an influenza model with treatment
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 07 January 2019, pp. 232-245
-
- Article
- Export citation
Lorentz Estimates for Weak Solutions of Quasi-linear Parabolic Equations with Singular Divergence-free Drifts
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 937-982
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Singular limits and properties of solutions of some degenerate elliptic and parabolic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 353-385
- Print publication:
- April 2019
-
- Article
- Export citation
Autonomous and non-autonomous unbounded attractors under perturbations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 877-903
- Print publication:
- August 2019
-
- Article
- Export citation
EXISTENCE AND BLOW-UP OF SOLUTIONS TO A PARABOLIC EQUATION WITH NONSTANDARD GROWTH CONDITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 11 December 2018, pp. 242-249
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Gradient Estimates for Spacelike Mean Curvature Flow with Boundary Conditions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 29 November 2018, pp. 459-469
-
- Article
- Export citation
Simulation of multiphase porous media flows with minimising movement and finite volume schemes
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 31 October 2018, pp. 1123-1152
-
- Article
- Export citation
Dynamics and asymptotic profiles of endemic equilibrium for two frequency-dependent SIS epidemic models with cross-diffusion
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 18 September 2018, pp. 26-56
-
- Article
- Export citation
On the avascular ellipsoidal tumour growth model within a nutritive environment
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 18 September 2018, pp. 111-142
-
- Article
- Export citation
OPTION PRICING UNDER THE KOBOL MODEL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 60 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 12 September 2018, pp. 175-190
-
- Article
-
- You have access
- Export citation
Time adaptive numerical solution of a highly non-linear degenerate cross-diffusion system arising in multi-species biofilm modelling
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 29 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 10 September 2018, pp. 1035-1061
-
- Article
-
- You have access
- Export citation
A Class of Parabolic Equations Driven by the Mean Curvature Flow
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 135-163
-
- Article
- Export citation
The effect of impurities on striped phases
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 20 August 2018, pp. 131-168
- Print publication:
- February 2019
-
- Article
- Export citation
ENTIRE SOLUTIONS OF A CURVATURE FLOW IN AN UNDULATING CYLINDER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 15 August 2018, pp. 137-147
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
MATHEMATICAL ANALYSIS OF COMBUSTION WAVES IN COMPETITIVE EXOTHERMIC REACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 19 July 2018, pp. 339-342
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
A REACTION–DIFFUSION–ADVECTION EQUATION WITH COMBUSTION NONLINEARITY ON THE HALF-LINE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 02 July 2018, pp. 277-285
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
Global dynamics and spreading speeds for a partially degenerate system with non-local dispersal in periodic habitats
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 22 June 2018, pp. 849-880
- Print publication:
- August 2018
-
- Article
- Export citation
Sharp decay estimates in a bioconvection model with quadratic degradation in bounded domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 5 / October 2018
- Published online by Cambridge University Press:
- 25 April 2018, pp. 939-955
- Print publication:
- October 2018
-
- Article
- Export citation
Classification of extinction profiles for a one-dimensional diffusive Hamilton–Jacobi equation with critical absorption
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 22 April 2018, pp. 559-574
- Print publication:
- June 2018
-
- Article
- Export citation