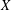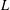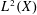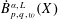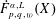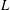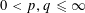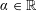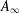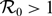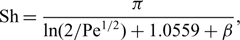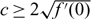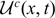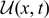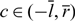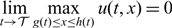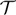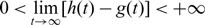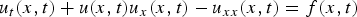Refine listing
Actions for selected content:
300 results in 35Kxx
WEIGHTED BESOV AND TRIEBEL–LIZORKIN SPACES ASSOCIATED WITH OPERATORS AND APPLICATIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 26 February 2020, e11
-
- Article
-
- You have access
- Open access
- Export citation
Spatial dynamics of a nonlocal model with periodic delay and competition
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 06 January 2020, pp. 1070-1100
-
- Article
- Export citation
Degenerate equations in a diffusion–precipitation model for clogging porous media
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 18 December 2019, pp. 1050-1069
-
- Article
-
- You have access
- Open access
- Export citation
Semi-analytical solution of a McKean–Vlasov equation with feedback through hitting a boundary
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 16 December 2019, pp. 1035-1068
-
- Article
- Export citation
Steady states and dynamics of a thin-film-type equation with non-conserved mass
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 22 November 2019, pp. 968-1001
-
- Article
- Export citation
Cops-on-the-dots: The linear stability of crime hotspots for a 1-D reaction-diffusion model of urban crime
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 11 November 2019, pp. 871-917
-
- Article
- Export citation
Global minimisers for anisotropic attractive–repulsive interactions
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 22 October 2019, pp. 854-870
-
- Article
- Export citation
Two components is too simple: an example of oscillatory Fisher–KPP system with three components
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 24 September 2019, pp. 3097-3120
- Print publication:
- December 2020
-
- Article
- Export citation
Small Péclet-number mass transport to a finite strip: An advection–diffusion–reaction model of surface-based biosensors
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 05 September 2019, pp. 763-781
-
- Article
- Export citation
Existence, uniqueness and stability of transition fronts of non-local equations in time heterogeneous bistable media
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 28 August 2019, pp. 601-645
-
- Article
- Export citation
Uniqueness and time oscillating behaviour of finite points blow-up solutions of the fast diffusion equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 09 August 2019, pp. 2849-2870
- Print publication:
- December 2020
-
- Article
- Export citation
Travelling waves in a reaction-diffusion system modelling farmer and hunter-gatherer interaction in the Neolithic transition in Europe
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 18 June 2019, pp. 470-510
-
- Article
- Export citation
Existence and uniqueness of monotone wavefronts in a nonlocal resource-limited model
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 07 May 2019, pp. 2462-2483
- Print publication:
- October 2020
-
- Article
- Export citation
Nonlinear systems coupled through multi-marginal transport problems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 April 2019, pp. 450-469
-
- Article
- Export citation
Global well-posedness of advective Lotka–Volterra competition systems with nonlinear diffusion
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 03 April 2019, pp. 2322-2348
- Print publication:
- October 2020
-
- Article
- Export citation
Entire solutions of the Fisher–KPP equation on the half line
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 26 March 2019, pp. 407-422
-
- Article
- Export citation
Pointwise stability of reaction diffusion fronts
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 2216-2254
- Print publication:
- October 2020
-
- Article
- Export citation
Asymptotic behaviour of solutions of Fisher–KPP equation with free boundaries in time-periodic environment
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 423-449
-
- Article
- Export citation
Evolution of interfaces for the nonlinear parabolic p-Laplacian-type reaction-diffusion equations. II. Fast diffusion vs. absorption
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 18 March 2019, pp. 385-406
-
- Article
- Export citation
On non-autonomously forced Burgers equation with periodic and Dirichlet boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 14 March 2019, pp. 2025-2054
- Print publication:
- August 2020
-
- Article
- Export citation