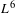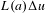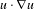Refine listing
Actions for selected content:
308 results in 35Kxx
Poincaré inequalities for Sobolev spaces with matrix-valued weights and applications to degenerate partial differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 22 April 2018, pp. 61-100
- Print publication:
- February 2019
-
- Article
- Export citation
Time-dependent attractors for non-autonomous non-local reaction–diffusion equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 5 / October 2018
- Published online by Cambridge University Press:
- 22 April 2018, pp. 957-981
- Print publication:
- October 2018
-
- Article
- Export citation
On regularity criteria of a weak solution to the three-dimensional magnetohydrodynamics equations in Lorentz space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 15 April 2018, pp. 593-604
- Print publication:
- June 2018
-
- Article
- Export citation
Evolution of non-simple closed curves in the area-preserving curvature flow
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 December 2017, pp. 659-668
- Print publication:
- June 2018
-
- Article
- Export citation
Analysis of Mathematics and Numerical Pattern Formation in Superdiffusive Fractional Multicomponent System
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 28 November 2017, pp. 1438-1460
- Print publication:
- December 2017
-
- Article
- Export citation
PARABOLIC CLASSICAL CURVATURE FLOWS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 338-357
-
- Article
-
- You have access
- Export citation
SEMI-ANALYTICAL SOLUTIONS FOR THE BRUSSELATOR REACTION–DIFFUSION MODEL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 59 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 23 October 2017, pp. 167-182
-
- Article
-
- You have access
- Export citation
A multi-species chemotaxis system: Lyapunov functionals, duality, critical mass
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 29 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 09 October 2017, pp. 515-542
-
- Article
- Export citation
A FUJITA-TYPE RESULT FOR A SEMILINEAR EQUATION IN HYPERBOLIC SPACE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 25 September 2017, pp. 420-429
-
- Article
-
- You have access
- Export citation
Blowup of Volterra Integro-Differential Equations and Applications to Semi-Linear Volterra Diffusion Equations
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 12 September 2017, pp. 737-759
- Print publication:
- November 2017
-
- Article
- Export citation
Some sharp results about the global existence and blowup of solutions to a class of pseudo-parabolic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 1311-1331
- Print publication:
- December 2017
-
- Article
- Export citation
Domain Decomposition Preconditioners for the System Generated by Discontinuous Galerkin Discretization of 2D-3T Heat Conduction Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 4 / October 2017
- Published online by Cambridge University Press:
- 28 July 2017, pp. 1069-1100
- Print publication:
- October 2017
-
- Article
- Export citation
SHORT TIME FULL ASYMPTOTIC EXPANSION OF HYPOELLIPTIC HEAT KERNEL AT THE CUT LOCUS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 10 July 2017, e16
-
- Article
-
- You have access
- Open access
- Export citation
On the Magneto-Heat Coupling Model for Large Power Transformers
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 06 July 2017, pp. 683-711
- Print publication:
- September 2017
-
- Article
- Export citation
Finite speed of propagation and waiting time for a thin-film Muskat problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 05 July 2017, pp. 813-830
- Print publication:
- August 2017
-
- Article
- Export citation
ILL-POSEDNESS FOR THE COMPRESSIBLE NAVIER–STOKES EQUATIONS WITH THE VELOCITY IN
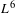 $L^{6}$ FRAMEWORK
$L^{6}$ FRAMEWORK
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 29 June 2017, pp. 829-854
- Print publication:
- July 2019
-
- Article
- Export citation
Heat Kernel Estimates Under the Ricci–Harmonic Map Flow
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 22 February 2017, pp. 831-857
-
- Article
- Export citation
An evolutional free-boundary problem of a reaction–diffusion–advection system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 13 February 2017, pp. 615-648
- Print publication:
- June 2017
-
- Article
- Export citation
Projected Finite Elements for Systems of Reaction-Diffusion Equations on Closed Evolving Spheroidal Surfaces
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 07 February 2017, pp. 718-747
- Print publication:
- March 2017
-
- Article
- Export citation
The Variational Iteration Method for an Inverse Problem of Finding a Source Parameter
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 18 January 2017, pp. 861-867
- Print publication:
- August 2017
-
- Article
- Export citation