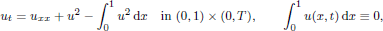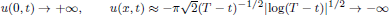Refine listing
Actions for selected content:
301 results in 35Kxx
Asymptotic behaviour of the lifespan of solutions for a semilinear heat equation in hyperbolic space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 30 August 2016, pp. 1091-1114
- Print publication:
- October 2016
-
- Article
- Export citation
DEVELOPMENT OF A PROCESS MODEL FOR THE PREDICTION OF ABSORBENT DEGRADATION DURING
 $\text{CO}_{2}$ CAPTURE
$\text{CO}_{2}$ CAPTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 16 August 2016, pp. 339-340
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
Aspects of Hadamard well-posedness for classes of non-Lipschitz semilinear parabolic partial differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 19 July 2016, pp. 777-832
- Print publication:
- August 2016
-
- Article
- Export citation
Dynamics of a susceptible–infected–susceptible epidemic reaction–diffusion model
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 19 July 2016, pp. 929-946
- Print publication:
- October 2016
-
- Article
- Export citation
An almost-periodic solution of Hasegawa–Wakatani equations with vanishing resistivity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 23 June 2016, pp. 983-1003
- Print publication:
- October 2016
-
- Article
- Export citation
RIESZ TRANSFORM ESTIMATES IN THE ABSENCE OFA PRESERVATION CONDITION AND APPLICATIONS TO THE DIRICHLET LAPLACIAN
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 08 March 2016, pp. 521-522
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
Optimal rates of convergence to the singular Barenblatt profile for the fast diffusion equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 309-324
- Print publication:
- April 2016
-
- Article
- Export citation
Application of the Level-Set Model with Constraints in Image Segmentation
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 9 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 15 February 2016, pp. 147-168
- Print publication:
- February 2016
-
- Article
- Export citation
THE QUENCHING OF SOLUTIONS OF A REACTION–DIFFUSION EQUATION WITH FREE BOUNDARIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 110-120
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
Short-time asymptotic expansions of semilinear evolution equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 07 January 2016, pp. 141-167
- Print publication:
- February 2016
-
- Article
- Export citation
GEOMETRIC SYMMETRY TECHNIQUES FOR PARTIAL DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 11 December 2015, pp. 342-344
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
UNIFORM BMO ESTIMATE OF PARABOLIC EQUATIONS AND GLOBAL WELL-POSEDNESS OF THE THERMISTOR PROBLEM
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 02 December 2015, e26
-
- Article
-
- You have access
- Open access
- Export citation
CONVERGENCE OF SOLUTIONS TO SOME ELLIPTIC EQUATIONS IN BOUNDED NEUMANN THIN DOMAINS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 20 November 2015, pp. 252-271
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
Interior Penalty Discontinuous Galerkin Based Isogeometric Analysis for Allen-Cahn Equations on Surfaces
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 5 / November 2015
- Published online by Cambridge University Press:
- 23 November 2015, pp. 1380-1416
- Print publication:
- November 2015
-
- Article
- Export citation
On a class of nonlinear anisotropic parabolic problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 22 October 2015, pp. 1-21
- Print publication:
- February 2016
-
- Article
- Export citation
An index theorem for end-periodic operators
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 2 / February 2016
- Published online by Cambridge University Press:
- 07 September 2015, pp. 399-444
- Print publication:
- February 2016
-
- Article
- Export citation
Lp -type pullback attractors for a semilinear heat equation on time-varying domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 5 / October 2015
- Published online by Cambridge University Press:
- 02 September 2015, pp. 1029-1052
- Print publication:
- October 2015
-
- Article
- Export citation
From homoclinics to quasi-periodic solutions for ordinary differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 5 / October 2015
- Published online by Cambridge University Press:
- 01 September 2015, pp. 1091-1114
- Print publication:
- October 2015
-
- Article
- Export citation
Cylindrically symmetric travelling fronts in a periodic reaction—diffusion equation with bistable nonlinearity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 5 / October 2015
- Published online by Cambridge University Press:
- 28 August 2015, pp. 1053-1090
- Print publication:
- October 2015
-
- Article
- Export citation
Global blow-up for a semilinear heat equation on a subspace
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 5 / October 2015
- Published online by Cambridge University Press:
- 24 August 2015, pp. 893-923
- Print publication:
- October 2015
-
- Article
- Export citation
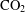
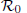 is defined for the model. We first prove that there exists a unique endemic equilibrium if
is defined for the model. We first prove that there exists a unique endemic equilibrium if 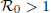 . We then consider the global attractivity of the disease-free equilibrium and the endemic equilibrium for two cases. If the disease transmission and recovery rates are constants or the diffusion rate of the susceptible individuals is equal to the diffusion rate of the infected individuals, we show that the disease-free equilibrium is globally attractive if
. We then consider the global attractivity of the disease-free equilibrium and the endemic equilibrium for two cases. If the disease transmission and recovery rates are constants or the diffusion rate of the susceptible individuals is equal to the diffusion rate of the infected individuals, we show that the disease-free equilibrium is globally attractive if 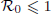 , while the endemic equilibrium is globally attractive if
, while the endemic equilibrium is globally attractive if 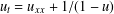
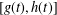
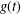
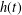
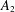
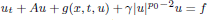
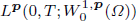 , where the data
, where the data