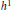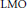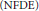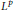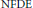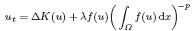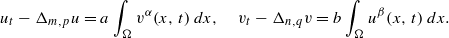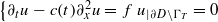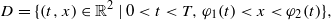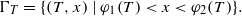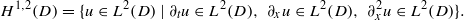Refine listing
Actions for selected content:
301 results in 35Kxx
DOMAIN PERTURBATION FOR PARABOLIC EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 16 December 2011, pp. 174-176
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
INHOMOGENEOUS PERIODIC PARABOLIC PROBLEMS WITH INDEFINITE DATA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 06 September 2011, pp. 516-524
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
Very slow grow-up of solutions of a semi-linear parabolic equation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 30 March 2011, pp. 381-400
-
- Article
-
- You have access
- Export citation
TRAVELLING WAVE SOLUTIONS FOR DOUBLY DEGENERATE REACTION–DIFFUSION EQUATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 52 / Issue 1 / July 2010
- Published online by Cambridge University Press:
- 10 March 2011, pp. 101-109
-
- Article
-
- You have access
- Export citation
ON THE STABILITY OF STATIONARY LINE AND GRIM REAPER IN PLANAR CURVATURE FLOW
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 07 February 2011, pp. 177-188
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
FOURTH ORDER GEOMETRIC EVOLUTION EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 18 November 2010, pp. 523-524
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
A NOTE ON THE NUMERICAL APPROACH FOR THE REACTION–DIFFUSION PROBLEM WITH A FREE BOUNDARY CONDITION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 51 / Issue 3 / January 2010
- Published online by Cambridge University Press:
- 13 October 2010, pp. 317-330
-
- Article
-
- You have access
- Export citation
ON THE ISOPERIMETRIC PROBLEM FOR THE LAPLACIAN WITH ROBIN AND WENTZELL BOUNDARY CONDITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 16 August 2010, pp. 348-350
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
TRAVELLING WAVE SOLUTIONS IN NONLOCAL REACTION–DIFFUSION SYSTEMS WITH DELAYS AND APPLICATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 51 / Issue 1 / July 2009
- Published online by Cambridge University Press:
- 09 March 2010, pp. 49-66
-
- Article
-
- You have access
- Export citation
Energy Functionals and Complex Monge–Ampère Equations
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 3 / July 2010
- Published online by Cambridge University Press:
- 10 February 2010, pp. 463-476
- Print publication:
- July 2010
-
- Article
- Export citation
Interior h1 Estimates for Parabolic Equations with LMO Coefficients
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 1 / 01 February 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 202-217
- Print publication:
- 01 February 2010
-
- Article
-
- You have access
- Export citation
Projectors on the Generalized Eigenspaces for Neutral Functional Differential Equations in Lp Spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 1 / 01 February 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 74-93
- Print publication:
- 01 February 2010
-
- Article
-
- You have access
- Export citation
Existence and blow-up of solutions for a non-local filtration and porous medium problem
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 12 January 2010, pp. 195-209
-
- Article
-
- You have access
- Export citation
MODELLING SEA ICE GROWTH
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 3 / January 2009
- Published online by Cambridge University Press:
- 03 November 2009, pp. 306-319
-
- Article
-
- You have access
- Export citation
A CONLEY INDEX CALCULATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 13 August 2009, pp. 510-520
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
Critical extinction and blow-up exponents for fast diffusive polytropic filtration equation with sources
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 28 May 2009, pp. 419-444
-
- Article
-
- You have access
- Export citation
HEAT KERNEL BOUNDS, POINCARÉ SERIES, AND L2 SPECTRUM FOR LOCALLY SYMMETRIC SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 73-86
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
GLOBAL EXISTENCE AND BLOW-UP FOR A NON-NEWTON POLYTROPIC FILTRATION SYSTEM WITH NONLOCAL SOURCE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 13-29
-
- Article
-
- You have access
- Export citation
REGULARITY OF A PARABOLIC EQUATION SOLUTION IN A NONSMOOTH AND UNBOUNDED DOMAIN
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 265-276
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
ON THE METHOD OF APPROXIMATION FOR EVOLUTIONARY INCLUSIONS OF PSEUDOMONOTONE TYPE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 115-143
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation