Refine listing
Actions for selected content:
1821 results in 60Gxx
Limit Theorems for Long-Memory Stochastic Volatility Models with Infinite Variance: Partial Sums and Sample Covariances
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 1113-1141
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Functional Relationships Between Price and Volatility Jumps and Their Consequences for Discretely Observed Data
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 30 January 2018, pp. 901-914
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
A Note on M/G/1 Vacation Systems with Sojourn Time Limits
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1194-1199
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
On the Exponential Ergodicity of Lévy-Driven Ornstein–Uhlenbeck Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 30 January 2018, pp. 990-1004
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Convex Duality in Mean-Variance Hedging Under Convex Trading Constraints
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 1084-1112
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Asymptotic Properties of the Approximate Inverse Estimator for Directional Distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 954-976
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
The Time to Ruin in Some Additive Risk Models with Random Premium Rates
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 30 January 2018, pp. 915-938
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Rare-Event Simulation of Heavy-Tailed Random Walks by Sequential Importance Sampling and Resampling
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 1173-1196
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Set Reconstruction by Voronoi Cells
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 938-953
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Asymptotics for Weighted Random Sums
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 1142-1172
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
On a new Class of Tempered Stable Distributions: Moments and Regular Variation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1015-1035
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
On the Functional Central Limit Theorem for Reversible Markov Chains with Nonlinear Growth of the Variance
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1091-1105
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Generalized Telegraph Process with Random Delays
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 850-865
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Random Marked Sets
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 603-616
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Uniqueness of Quasistationary Distributions and Discrete Spectra when ∞ is an Entrance Boundary and 0 is Singular
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 719-730
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Optimal Stopping Problems for Asset Management
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 655-677
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Tail Behavior of Randomly Weighted Sums
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 794-814
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Tightness for Maxima of Generalized Branching Random Walks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 652-670
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Predicting the Supremum: Optimality of ‘Stop at Once or Not at All’
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 806-820
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
A New Proof of the Wiener-Hopf Factorization via Basu's Theorem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 876-882
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
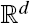 of intensity λ>0, define the Poisson–Voronoi approximation
of intensity λ>0, define the Poisson–Voronoi approximation 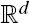 . Unlike for random fields, the mark covariance function of a random marked set is in general not positive definite. This implies that in many situations the use of simple geostatistical methods appears to be questionable. Surprisingly, for a special class of processes based on Gaussian random fields, we do have positive definiteness for the corresponding mark covariance function and mark correlation function.
. Unlike for random fields, the mark covariance function of a random marked set is in general not positive definite. This implies that in many situations the use of simple geostatistical methods appears to be questionable. Surprisingly, for a special class of processes based on Gaussian random fields, we do have positive definiteness for the corresponding mark covariance function and mark correlation function.