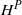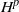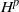Refine listing
Actions for selected content:
1821 results in 60Gxx
The Class of Tenable Zero-Balanced Pólya Urn Schemes: Characterization and Gaussian Phases
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 702-728
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
First Passage Time of Skew Brownian Motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 685-696
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
The Class of Distributions Associated with the Generalized Pollaczek-Khinchine Formula
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 883-887
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
On Exact Sampling of Nonnegative Infinitely Divisible Random Variables
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 842-873
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Fractional Brownian Motion with H < 1/2 as a Limit of Scheduled Traffic
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 710-718
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Spatial Stit Tessellations: Distributional Results for I-Segments
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 635-654
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Exit Problems for Reflected Markov-Modulated Brownian Motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 697-709
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
STATISTICAL CAUSALITY AND STABLE SUBSPACES OF
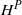 $H^P$
$H^P$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 01 August 2012, pp. 17-25
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
Backward Coalescence Times for Perfect Simulation of Chains with Infinite Memory
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 319-337
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
On Optimal Stopping Problems for Matrix-Exponential Jump-Diffusion Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 531-548
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Asymptotic Dependence for Light-Tailed Homothetic Densities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 506-527
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Continuous-Time Skewed Multifractal Processes as a Model for Financial Returns
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 482-502
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Fractional Relaxation Equations and Brownian Crossing Probabilities of a Random Boundary
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 479-505
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
On Rice's Formula for Stationary Multivariate Piecewise Smooth Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 351-363
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
On the Joint Behavior of Types of Coupons in Generalized Coupon Collection
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 429-451
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Occupation Times for Markov-Modulated Brownian Motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 549-565
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
An Inverse Gamma Activity Time Process with Noninteger Parameters and a Self-Similar Limit
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 441-450
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Sample Path Optimal Policies for Serial Lines with Flexible Workers
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 582-589
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
The Smooth-Fit Property in an Exponential Lévy Model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 137-149
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Approximating Multivariate Tempered Stable Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 167-183
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation