Refine listing
Actions for selected content:
1822 results in 60Gxx
Approximating Multivariate Tempered Stable Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 167-183
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Pareto Lévy Measures and Multivariate Regular Variation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 117-138
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Asymptotic Conditional Distribution of Exceedance Counts
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 270-291
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Transforming Spatial Point Processes into Poisson Processes Using Random Superposition
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 42-62
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Phase-Type Distributions and Optimal Stopping for Autoregressive Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 22-39
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Persistence and Equilibria of Branching Populations with Exponential Intensity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 226-244
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Card Counting in Continuous Time
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 184-198
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
A Note on the Dependence Structure of the Two-State Markovian Arrival Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 295-302
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Rational Processes Related to Communicating Markov Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 40-59
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
A Fourier Approach for the Level Crossings of Shot Noise Processes with Jumps
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 100-113
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Optimal Control with Absolutely Continuous Strategies for Spectrally Negative Lévy Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 150-166
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
The Transparent Dead Leaves Model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 1-20
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
INTEGRAL EQUATION METHODS IN CHANGE-POINT DETECTION PROBLEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 28 February 2012, pp. 518-520
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Dimension reduction and homogenization of random degenerate operators. Part I
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 January 2012, pp. 1-22
-
- Article
-
- You have access
- Export citation
Moments of Random Sums and Robbins' Problem of Optimal Stopping
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 4 / December 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1197-1199
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
Tail behavior of multivariate lévy-driven mixed moving average processes and supOU Stochastic Volatility Models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 4 / December 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1109-1135
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
On the Monitoring Error of the Supremum of a Normal Jump Diffusion Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 4 / December 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1021-1034
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
Ruin Probability with Parisian Delay for a Spectrally Negative Lévy Risk Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 4 / December 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 984-1002
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
Connecting discrete and continuous lookback or hindsight options in exponential Lévy models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 4 / December 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1136-1165
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
A Generalized Coupon Collector Problem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 4 / December 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1081-1094
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
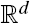 with Lévy measure Π, emphasizing the dependence between jumps of its components. By transforming the one-dimensional marginal Lévy measures to those of a standard 1-stable Lévy process, we decouple the marginal Lévy measures from the dependence structure. The dependence between the jumps is modeled by a so-called
with Lévy measure Π, emphasizing the dependence between jumps of its components. By transforming the one-dimensional marginal Lévy measures to those of a standard 1-stable Lévy process, we decouple the marginal Lévy measures from the dependence structure. The dependence between the jumps is modeled by a so-called 