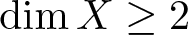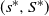Refine listing
Actions for selected content:
336 results in 60Hxx
Intrinsic stochastic differential equations and the extended Itô formula on manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 12 December 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NEW PROOF OF THE SINGULAR CONTINUITY OF THE MINKOWSKI
 $?$-FUNCTION
$?$-FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-6
-
- Article
- Export citation
Stochastic Volterra integral equations with ranks as scaling limits of parallel infinite-server queues under weighted shortest queue policy
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 02 December 2025, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DYNAMICS OF NONLOCAL KURAMOTO–SIVASHINSHY EQUATIONS WITH MULTIPLICATIVE WHITE NOISE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 23 October 2025, e34
-
- Article
-
- You have access
- HTML
- Export citation
Mixed-state branching evolution for cell division models
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 29 September 2025, pp. 1-22
-
- Article
- Export citation
Explicit pathwise expansion for multivariate diffusions with applications
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 29 September 2025, pp. 1-34
-
- Article
- Export citation
Well-posedness and averaging principle for non-Gaussian McKean–Vlasov stochastic differential equations with locally Lipschitz coefficients
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-44
-
- Article
- Export citation
Pullback measure attractors for stochastic p-Laplacian parabolic equations on thin domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 05 August 2025, pp. 1-28
-
- Article
- Export citation
STOCHASTIC MODELLING OF WILDFIRE SPREAD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 28 July 2025, pp. 399-400
- Print publication:
- October 2025
-
- Article
-
- You have access
- HTML
- Export citation
Optimal multiple stopping problem with irregular reward
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 14 July 2025, pp. 1607-1622
- Print publication:
- December 2025
-
- Article
- Export citation
Limit theorems of stochastic differential equations with jumps
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 16 June 2025, pp. 1429-1445
- Print publication:
- December 2025
-
- Article
- Export citation
Averaging principle for the fast–slow McKean–Vlasov stochastic differential equations driven by mixed fractional Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 05 June 2025, pp. 1260-1279
- Print publication:
- December 2025
-
- Article
- Export citation
Remark on the local well-posedness for NLS with the modulated dispersion
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-12
-
- Article
- Export citation
Approximation of the invariant measure for stable stochastic differential equations by the Euler–Maruyama scheme with decreasing step sizes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 31 March 2025, pp. 1000-1030
- Print publication:
- September 2025
-
- Article
- Export citation
Optimal inventory control with state-dependent jumps
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1360-1391
- Print publication:
- December 2025
-
- Article
- Export citation
MICRO-MACRO PARAREAL, FROM ORDINARY DIFFERENTIAL EQUATIONS TO STOCHASTIC DIFFERENTIAL EQUATIONS AND BACK AGAIN
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 17 March 2025, e13
-
- Article
- Export citation
Two dynamical approaches to the notion of exponential separation for random systems of delay differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic expansion of the invariant measure for Markov-modulated ODEs at high frequency
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 30 January 2025, pp. 898-924
- Print publication:
- September 2025
-
- Article
- Export citation
Single-item continuous-review inventory models with random supplies
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 134-170
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Localization in the random XXZ quantum spin chain
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 03 January 2025, e129
-
- Article
-
- You have access
- Open access
- HTML
- Export citation