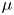 $\mu$-constant deformations admit simultaneous embedded resolutions
$\mu$-constant deformations admit simultaneous embedded resolutions
 $\mathscr{D}$-modules and index theorems
$\mathscr{D}$-modules and index theorems
 $\mathbb{Q}$-DIVISORS,
$\mathbb{Q}$-DIVISORS, 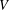 $V$-FILTRATION, AND MINIMAL EXPONENT
$V$-FILTRATION, AND MINIMAL EXPONENT