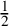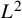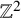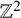Refine listing
Actions for selected content:
78 results in 82Cxx
Probabilistic operators for non-attacking tableaux and a compact formula for the symmetric Macdonald polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 15 September 2025, e146
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Colored interacting particle systems on the ring: Stationary measures from Yang–Baxter equations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 03 October 2025, pp. 1855-1922
- Print publication:
- August 2025
-
- Article
- Export citation
Critical configurations of the hard-core model on square grid graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 04 February 2025, pp. 445-485
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Localization in the random XXZ quantum spin chain
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 03 January 2025, e129
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Scaling limit of soliton lengths in a multicolor box-ball system
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 December 2024, e120
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topological structures of large-scale interacting systems via uniform functions and forms
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 November 2024, e107
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random growth via gradient flow aggregation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 735-755
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Recent kernel methods for interacting particle systems: first numerical results
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 11 November 2024, pp. 464-489
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN INVESTIGATION INTO RECENT THEORIES OF RELAXATION TOWARDS EQUILIBRIUM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 27 September 2024, pp. 570-571
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
Relationships between two linearizations of the box-ball system: Kerov–Kirillov–Reschetikhin bijection and slot configuration
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 May 2024, e55
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unified framework for the separation property in binary phase-segregation processes with singular entropy densities
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 09 May 2024, pp. 40-67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Emergent behaviours of a non-abelian quantum synchronisation model over the unitary group
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 30 April 2024, pp. 328-348
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniform propagation of chaos for a dollar exchange econophysics model
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 22 April 2024, pp. 27-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Macroscopic limit of a Fokker-Planck model of swarming rigid bodies
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 19 April 2024, pp. 349-397
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A sufficient condition for the quasipotential to be the rate function of the invariant measure of countable-state mean-field interacting particle systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 21 March 2024, pp. 960-1003
- Print publication:
- September 2024
-
- Article
- Export citation
Network-based kinetic models: Emergence of a statistical description of the graph topology
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 02 February 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Thermalization in Kitaev’s quantum double models via tensor network techniques
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 28 November 2023, e107
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Collapse and diffusion in harmonic activation and transport
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 27 September 2023, e85
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fluctuations of the local times of the self-repelling random walk with directed edges
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 15 September 2023, pp. 545-586
- Print publication:
- June 2024
-
- Article
- Export citation
A rigorous derivation of the Hamiltonian structure for the Vlasov equation
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 September 2023, e77
-
- Article
-
- You have access
- Open access
- HTML
- Export citation