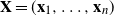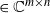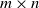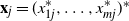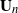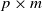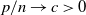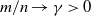Refine listing
Actions for selected content:
106 results in 62Hxx
SPATIAL STATISTICAL INFERENCE FROM A DECISION-THEORETIC VIEWPOINT WITH APPLICATION TO NON-GAUSSIAN ENVIRONMENTAL DATA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 10 December 2025, pp. 1-2
-
- Article
-
- You have access
- HTML
- Export citation
Negative dependence in knockout tournaments
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-16
-
- Article
-
- You have access
- HTML
- Export citation
Infinitely resizable urn models
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 24 November 2025, pp. 1-35
-
- Article
- Export citation
VARIABLE SELECTION IN MULTIVARIATE DATA BY ANALYSIS OF DATA PATTERN
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 11 August 2025, pp. 572-573
- Print publication:
- December 2025
-
- Article
-
- You have access
- HTML
- Export citation
Estranged facets and k-facets of Gaussian random point sets
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 02 April 2025, pp. 859-875
- Print publication:
- September 2025
-
- Article
- Export citation
EXPLORING OUT-OF-SAMPLE PREDICTION AND SPATIAL DEPENDENCY FOR COMPLEX BIG DATA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 380-382
- Print publication:
- April 2025
-
- Article
-
- You have access
- HTML
- Export citation
On a class of bivariate distributions built of q-ultraspherical polynomials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1-34
-
- Article
- Export citation
An MBO method for modularity optimisation based on total variation and signless total variation
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-83
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Almost exact recovery in noisy semi-supervised learning
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 39 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 11 November 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The dutch draw: constructing a universal baseline for binary classification problems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 19 September 2024, pp. 475-493
- Print publication:
- June 2025
-
- Article
- Export citation
Exact recovery of community detection in k-community Gaussian mixture models
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 491-523
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The limiting spectral distribution of large random permutation matrices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 12 April 2024, pp. 1301-1318
- Print publication:
- December 2024
-
- Article
- Export citation
The unified extropy and its versions in classical and Dempster–Shafer theories
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 23 October 2023, pp. 685-696
- Print publication:
- June 2024
-
- Article
- Export citation
ON THE N-POINT CORRELATION OF VAN DER CORPUT SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 15 September 2023, pp. 471-475
- Print publication:
- June 2024
-
- Article
- Export citation
Exchangeable FGM copulas
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 24 August 2023, pp. 205-234
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTRACTING FEATURES FROM EIGENFUNCTIONS: HIGHER CHEEGER CONSTANTS AND SPARSE EIGENBASIS APPROXIMATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 22 August 2023, pp. 511-512
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
Asymptotic expansion of the expected Minkowski functional for isotropic central limit random fields
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 14 July 2023, pp. 1390-1414
- Print publication:
- December 2023
-
- Article
- Export citation
Asymptotic results on tail moment and tail central moment for dependent risks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 08 May 2023, pp. 1116-1143
- Print publication:
- December 2023
-
- Article
- Export citation
How do empirical estimators of popular risk measures impact pro-cyclicality?
- Part of
-
- Journal:
- Annals of Actuarial Science / Volume 17 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 29 March 2023, pp. 547-579
-
- Article
- Export citation
The Berkelmans–Pries dependency function: A generic measure of dependence between random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 23 March 2023, pp. 1115-1135
- Print publication:
- December 2023
-
- Article
- Export citation