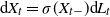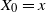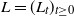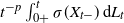Refine search
Actions for selected content:
52379 results in Statistics and Probability
Trichinella infection in Serbia from 2011 to 2020: a success story in the field of One Health
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 19 January 2023, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A large A(H3N2) influenza outbreak with a high attack rate in a drug user community in Italy, April 2022
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 19 January 2023, e36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PES volume 37 issue 1 Cover
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 18 January 2023, p. f1
-
- Article
-
- You have access
- Export citation
Relationships between cumulative entropy/extropy, Gini mean difference and probability weighted moments
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 18 January 2023, pp. 28-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Critical branching as a pure death process coming down from infinity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 18 January 2023, pp. 607-628
- Print publication:
- June 2023
-
- Article
- Export citation
Use of portable air purifiers to reduce aerosols in hospital settings and cut down the clinical backlog
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 18 January 2023, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Parking functions: interdisciplinary connections
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 17 January 2023, pp. 768-792
- Print publication:
- September 2023
-
- Article
- Export citation
RELEVANT MOMENT SELECTION UNDER MIXED IDENTIFICATION STRENGTH
-
- Journal:
- Econometric Theory / Volume 40 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 16 January 2023, pp. 1003-1064
-
- Article
-
- You have access
- Open access
- Export citation
Predicting the last zero before an exponential time of a spectrally negative Lévy process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 16 January 2023, pp. 611-642
- Print publication:
- June 2023
-
- Article
- Export citation
Response to COVID-19 in Lebanon: update, challenges and lessons learned
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 16 January 2023, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transition density of an infinite-dimensional diffusion with the jack parameter
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 16 January 2023, pp. 797-811
- Print publication:
- September 2023
-
- Article
- Export citation
Index
-
- Book:
- Discrete Quantum Walks on Graphs and Digraphs
- Published online:
- 23 December 2022
- Print publication:
- 12 January 2023, pp 137-138
-
- Chapter
- Export citation
Glossary
-
- Book:
- Discrete Quantum Walks on Graphs and Digraphs
- Published online:
- 23 December 2022
- Print publication:
- 12 January 2023, pp 131-131
-
- Chapter
- Export citation
Preface
-
- Book:
- Discrete Quantum Walks on Graphs and Digraphs
- Published online:
- 23 December 2022
- Print publication:
- 12 January 2023, pp xi-xii
-
- Chapter
- Export citation
4 - Averaging
-
- Book:
- Discrete Quantum Walks on Graphs and Digraphs
- Published online:
- 23 December 2022
- Print publication:
- 12 January 2023, pp 41-58
-
- Chapter
- Export citation
5 - Covers and Embeddings
-
- Book:
- Discrete Quantum Walks on Graphs and Digraphs
- Published online:
- 23 December 2022
- Print publication:
- 12 January 2023, pp 59-76
-
- Chapter
- Export citation
3 - Applications
-
- Book:
- Discrete Quantum Walks on Graphs and Digraphs
- Published online:
- 23 December 2022
- Print publication:
- 12 January 2023, pp 20-40
-
- Chapter
- Export citation
References
-
- Book:
- Discrete Quantum Walks on Graphs and Digraphs
- Published online:
- 23 December 2022
- Print publication:
- 12 January 2023, pp 132-136
-
- Chapter
- Export citation
Short-time behavior of solutions to Lévy-driven stochastic differential equations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 January 2023, pp. 765-780
- Print publication:
- September 2023
-
- Article
- Export citation
Invariant Galton–Watson trees: metric properties and attraction with respect to generalized dynamical pruning
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 12 January 2023, pp. 643-671
- Print publication:
- June 2023
-
- Article
- Export citation