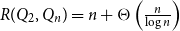Refine search
Actions for selected content:
52379 results in Statistics and Probability
Explainable machine learning for public policy: Use cases, gaps, and research directions
-
- Journal:
- Data & Policy / Volume 5 / 2023
- Published online by Cambridge University Press:
- 20 February 2023, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A closed-form approximation for pricing spread options on futures under a mean-reverting spot price model with multiscale stochastic volatility
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 20 February 2023, pp. 168-188
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transmission trends of the global COVID-19 pandemic with combined effects of adaptive behaviours and vaccination
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 20 February 2023, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Characteristics of patients with SARS-COV-2 PCR re-positivity after recovering from COVID-19
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 17 February 2023, e34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Poset Ramsey numbers: large Boolean lattice versus a fixed poset
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 17 February 2023, pp. 638-653
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Method-of-moments estimators of a scale parameter based on samples from a coherent system
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 16 February 2023, pp. 150-167
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A simple European option pricing formula with a skew Brownian motion – ERRATUM
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 16 February 2023, p. 226
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effectiveness of quadrivalent HPV vaccination in reducing vaccine-type and nonvaccine-type high risk HPV infection
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 15 February 2023, e37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Estimating the share of SARS-CoV-2-immunologically naïve individuals in Germany up to June 2022
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 15 February 2023, e38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiple random walks on graphs: mixing few to cover many
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 15 February 2023, pp. 594-637
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Public health interventions successfully mitigated multiple incursions of SARS-CoV-2 Delta variant in the Australian Capital Territory
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 14 February 2023, e30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ECT volume 39 issue 1 Cover and Back matter
-
- Journal:
- Econometric Theory / Volume 39 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 14 February 2023, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Random feedback shift registers and the limit distribution for largest cycle lengths
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 14 February 2023, pp. 559-593
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exactly solvable urn models under random replacement schemes and their applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 14 February 2023, pp. 835-854
- Print publication:
- September 2023
-
- Article
- Export citation
ECT volume 39 issue 1 Cover and Front matter
-
- Journal:
- Econometric Theory / Volume 39 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 14 February 2023, pp. f1-f2
-
- Article
-
- You have access
- Export citation
APR volume 55 issue 1 Cover and Back matter
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 13 February 2023, pp. b1-b2
- Print publication:
- March 2023
-
- Article
-
- You have access
- Export citation
Prevalence and persistence of Neisseria meningitidis carriage in Swedish university students
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 13 February 2023, e25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Searching for coherence in a fragmented field: Temporal and keywords network analysis in political science
-
- Journal:
- Network Science / Volume 11 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 13 February 2023, pp. 113-142
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
APR volume 55 issue 1 Cover and Front matter
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 13 February 2023, pp. f1-f2
- Print publication:
- March 2023
-
- Article
-
- You have access
- Export citation
Random multi-hooking networks
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 13 February 2023, pp. 100-114
-
- Article
-
- You have access
- Open access
- HTML
- Export citation