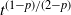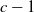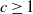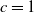Refine search
Actions for selected content:
52379 results in Statistics and Probability
Bounds on the mean and squared coefficient of variation of phase-type distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 880-889
- Print publication:
- December 2021
-
- Article
- Export citation
Multitype branching process with non-homogeneous Poisson and contagious Poisson immigration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 1007-1042
- Print publication:
- December 2021
-
- Article
- Export citation
A stochastic matching model on hypergraphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 951-980
- Print publication:
- December 2021
-
- Article
- Export citation
Assortment of kaempferol and zinc gluconate improves noise-induced biochemical imbalance and deficits in body weight gain
-
- Journal:
- Experimental Results / Volume 2 / 2021
- Published online by Cambridge University Press:
- 22 November 2021, e37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A restaurant process with cocktail bar and relations to the three-parameter Mittag–Leffler distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 978-1006
- Print publication:
- December 2021
-
- Article
- Export citation
Sparse regular variation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 1115-1148
- Print publication:
- December 2021
-
- Article
- Export citation
JPR volume 58 issue 4 Cover and Front matter
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. f1-f2
- Print publication:
- December 2021
-
- Article
-
- You have access
- Export citation
Approximations of geometrically ergodic reversible markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 981-1022
- Print publication:
- December 2021
-
- Article
- Export citation
APR volume 53 issue 4 Cover and Back matter
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. b1-b2
- Print publication:
- December 2021
-
- Article
-
- You have access
- Export citation
Clustering in preferential attachment random graphs with edge-step
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 890-908
- Print publication:
- December 2021
-
- Article
- Export citation
Two poisson limit theorems for the coupon collector’s problem with group drawings
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 966-977
- Print publication:
- December 2021
-
- Article
- Export citation
Shot noise processes with randomly delayed cluster arrivals and dependent noises in the large-intensity regime
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 1190-1221
- Print publication:
- December 2021
-
- Article
- Export citation
APR volume 53 issue 4 Cover and Front matter
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. f1-f2
- Print publication:
- December 2021
-
- Article
-
- You have access
- Export citation
Asymptotic behavior of projections of supercritical multi-type continuous-state and continuous-time branching processes with immigration
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 1023-1060
- Print publication:
- December 2021
-
- Article
- Export citation
A value-at-risk approach to mis-estimation risk
-
- Journal:
- British Actuarial Journal / Volume 26 / 2021
- Published online by Cambridge University Press:
- 19 November 2021, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pricing insurance policies with offsetting relationship – ERRATUM
-
- Journal:
- Annals of Actuarial Science / Volume 16 / Issue 2 / July 2022
- Published online by Cambridge University Press:
- 19 November 2021, p. 288
-
- Article
-
- You have access
- HTML
- Export citation
Molecular epidemiology of hepatitis B virus genotypes and subgenotypes in ethnic minority populations, Yunnan province, China
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 17 November 2021, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Knowledge politics in the smart city: A case study of strategic urban planning in Cambridge, UK
-
- Journal:
- Data & Policy / Volume 3 / 2021
- Published online by Cambridge University Press:
- 17 November 2021, e31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A WILD BOOTSTRAP FOR DEPENDENT DATA
-
- Journal:
- Econometric Theory / Volume 39 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 17 November 2021, pp. 264-289
-
- Article
- Export citation
Societal activities associated with SARS-CoV-2 infection: a case-control study in Denmark, November 2020
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 17 November 2021, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation