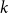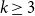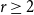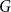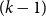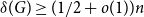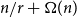Refine search
Actions for selected content:
52379 results in Statistics and Probability
9 - POMDPs in Controlled Sensing and Sensor Scheduling
- from Part II - POMDPs. Models, Algorithms and Applications
-
- Book:
- Partially Observed Markov Decision Processes
- Published online:
- 16 May 2025
- Print publication:
- 05 June 2025, pp 231-254
-
- Chapter
- Export citation
16 - Stochastic Optimization and Gradient Estimation
- from Part IV - Stochastic Gradient Algorithms and Reinforcement Learning
-
- Book:
- Partially Observed Markov Decision Processes
- Published online:
- 16 May 2025
- Print publication:
- 05 June 2025, pp 425-444
-
- Chapter
- Export citation
Part II - POMDPs. Models, Algorithms and Applications
-
- Book:
- Partially Observed Markov Decision Processes
- Published online:
- 16 May 2025
- Print publication:
- 05 June 2025, pp 163-164
-
- Chapter
- Export citation
Preface to Revised Edition
-
- Book:
- Partially Observed Markov Decision Processes
- Published online:
- 16 May 2025
- Print publication:
- 05 June 2025, pp xii-xiv
-
- Chapter
- Export citation
4 - Algorithms for Maximum Likelihood Parameter Estimation
- from Part I - Stochastic Models and Bayesian Inference
-
- Book:
- Partially Observed Markov Decision Processes
- Published online:
- 16 May 2025
- Print publication:
- 05 June 2025, pp 71-90
-
- Chapter
- Export citation
12 - Monotonicity of Value Function for POMDPs
- from Part III - POMDP Structural Results
-
- Book:
- Partially Observed Markov Decision Processes
- Published online:
- 16 May 2025
- Print publication:
- 05 June 2025, pp 312-326
-
- Chapter
- Export citation
Contents
-
- Book:
- Partially Observed Markov Decision Processes
- Published online:
- 16 May 2025
- Print publication:
- 05 June 2025, pp v-xi
-
- Chapter
- Export citation
5 - Multiagent Sensing: Social Learning and Data Incest
- from Part I - Stochastic Models and Bayesian Inference
-
- Book:
- Partially Observed Markov Decision Processes
- Published online:
- 16 May 2025
- Print publication:
- 05 June 2025, pp 91-113
-
- Chapter
- Export citation
Cutoff for the logistic SIS epidemic model with self-infection
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 04 June 2025, pp. 1456-1483
- Print publication:
- December 2025
-
- Article
- Export citation
Moderate deviations for weight-dependent random connection models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 04 June 2025, pp. 1406-1428
- Print publication:
- December 2025
-
- Article
- Export citation
Percolation in lattice k-neighbor graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 03 June 2025, pp. 1475-1492
- Print publication:
- December 2025
-
- Article
- Export citation
Facing the ambiguities of participation in data-driven projects: a systematic literature review
-
- Journal:
- Data & Policy / Volume 7 / 2025
- Published online by Cambridge University Press:
- 03 June 2025, e41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Recurring spoken term discovery in the zero-resource constraint using diagonal patterns
-
- Journal:
- Data-Centric Engineering / Volume 6 / 2025
- Published online by Cambridge University Press:
- 02 June 2025, e28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Case–control study of leptospirosis in Aotearoa New Zealand reveals behavioural, occupational, and environmental risk factors
-
- Journal:
- Epidemiology & Infection / Volume 153 / 2025
- Published online by Cambridge University Press:
- 02 June 2025, e67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tight Hamilton cycles with high discrepancy
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 30 May 2025, pp. 565-584
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Legionnaires’ disease outbreak linked to a cold-water source in Yorkshire, 2022
-
- Journal:
- Epidemiology & Infection / Volume 153 / 2025
- Published online by Cambridge University Press:
- 30 May 2025, e66
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Random Matrix Theory, Interacting Particle Systems, and Integrable Systems
-
- Published online:
- 29 May 2025
- Print publication:
- 15 December 2014
On the last zero process with an application in corporate bankruptcy
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 28 May 2025, pp. 1-48
-
- Article
- Export citation
Quantifying the direct and indirect components of COVID-19 vaccine effectiveness during the Delta variant era – ERRATUM
-
- Journal:
- Epidemiology & Infection / Volume 153 / 2025
- Published online by Cambridge University Press:
- 28 May 2025, e65
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE ECONOMETRIC THEORY AWARDS 2025
-
- Journal:
- Econometric Theory / Volume 41 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 28 May 2025, p. 994
-
- Article
-
- You have access
- Export citation