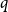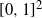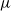Refine search
Actions for selected content:
52346 results in Statistics and Probability
Generating preferential attachment graphs via a Pólya urn with expanding colors
-
- Journal:
- Network Science / Volume 12 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 08 April 2024, pp. 139-159
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Buffon’s problem determines Gaussian curvature in three geometries
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 08 April 2024, pp. 1127-1138
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Decreased risk of non-influenza respiratory infection after influenza B virus infection in children
-
- Journal:
- Epidemiology & Infection / Volume 152 / 2024
- Published online by Cambridge University Press:
- 08 April 2024, e60
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algorithms for the ferromagnetic Potts model on expanders
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 05 April 2024, pp. 487-517
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Super-replication of life-contingent options under the Black–Scholes framework
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 05 April 2024, pp. 1263-1277
- Print publication:
- December 2024
-
- Article
- Export citation
Coherent distributions on the square–extreme points and asymptotics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 05 April 2024, pp. 1240-1262
- Print publication:
- December 2024
-
- Article
- Export citation
Signature-based validation of real-world economic scenarios
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 54 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 04 April 2024, pp. 410-440
- Print publication:
- May 2024
-
- Article
- Export citation
An extreme worst-case risk measure by expectile
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1195-1214
- Print publication:
- December 2024
-
- Article
- Export citation
Convergence of the height process of supercritical Galton–Watson forests with an application to the configuration model in the critical window
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1064-1105
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topological reconstruction of compact supports of dependent stationary random variables
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1339-1369
- Print publication:
- December 2024
-
- Article
- Export citation
AN ASYMPTOTIC THEORY FOR JUMP DIFFUSION MODELS
-
- Journal:
- Econometric Theory / Volume 41 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 02 April 2024, pp. 844-906
-
- Article
-
- You have access
- Open access
- Export citation
Data-driven healthcare indicators via precision gaming: With application to India
-
- Journal:
- Data & Policy / Volume 6 / 2024
- Published online by Cambridge University Press:
- 01 April 2024, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Impact of COVID-19 on the degree of compliance with hand hygiene: a repeated cross-sectional study
-
- Journal:
- Epidemiology & Infection / Volume 152 / 2024
- Published online by Cambridge University Press:
- 01 April 2024, e69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TIME-VARYING PARAMETER REGRESSIONS WITH STATIONARY PERSISTENT DATA
-
- Journal:
- Econometric Theory / Volume 41 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 01 April 2024, pp. 817-843
-
- Article
-
- You have access
- Open access
- Export citation
Smoothness and monotonicity constraints for neural networks using ICEnet
-
- Journal:
- Annals of Actuarial Science / Volume 18 / Issue 3 / November 2024
- Published online by Cambridge University Press:
- 01 April 2024, pp. 712-739
-
- Article
- Export citation
Deployment of digital technologies in African cities: emerging issues and policy recommendations for local governments
-
- Journal:
- Data & Policy / Volume 6 / 2024
- Published online by Cambridge University Press:
- 01 April 2024, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Real-time evaluation of a multi-agency TB-screening event for persons experiencing homelessness in a town with a low incidence of TB in England
-
- Journal:
- Epidemiology & Infection / Volume 152 / 2024
- Published online by Cambridge University Press:
- 01 April 2024, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A digital twin for ship structures—R&D project in Japan
- Part of
-
- Journal:
- Data-Centric Engineering / Volume 5 / 2024
- Published online by Cambridge University Press:
- 27 March 2024, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A spectrum of physics-informed Gaussian processes for regression in engineering
- Part of
-
- Journal:
- Data-Centric Engineering / Volume 5 / 2024
- Published online by Cambridge University Press:
- 27 March 2024, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Constrained optimal stopping under a regime-switching model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 27 March 2024, pp. 1220-1239
- Print publication:
- December 2024
-
- Article
- Export citation