We study the dynamics of a reaction–diffusion–advection equation 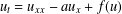 $u_{t}=u_{xx}-au_{x}+f(u)$ on the right half-line with Robin boundary condition
$u_{t}=u_{xx}-au_{x}+f(u)$ on the right half-line with Robin boundary condition 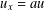 $u_{x}=au$ at
$u_{x}=au$ at 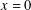 $x=0$, where
$x=0$, where 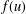 $f(u)$ is a combustion nonlinearity. We show that, when
$f(u)$ is a combustion nonlinearity. We show that, when 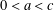 $0<a<c$ (where
$0<a<c$ (where  $c$ is the travelling wave speed of
$c$ is the travelling wave speed of 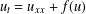 $u_{t}=u_{xx}+f(u)$),
$u_{t}=u_{xx}+f(u)$),  $u$ converges in the
$u$ converges in the 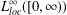 $L_{loc}^{\infty }([0,\infty ))$ topology either to
$L_{loc}^{\infty }([0,\infty ))$ topology either to 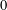 $0$ or to a positive steady state; when
$0$ or to a positive steady state; when 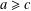 $a\geq c$, a solution
$a\geq c$, a solution  $u$ starting from a small initial datum tends to
$u$ starting from a small initial datum tends to 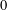 $0$ in the
$0$ in the 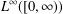 $L^{\infty }([0,\infty ))$ topology, but this is not true for a solution starting from a large initial datum; when
$L^{\infty }([0,\infty ))$ topology, but this is not true for a solution starting from a large initial datum; when 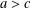 $a>c$, such a solution converges to
$a>c$, such a solution converges to 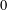 $0$ in
$0$ in 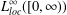 $L_{loc}^{\infty }([0,\infty ))$ but not in
$L_{loc}^{\infty }([0,\infty ))$ but not in 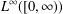 $L^{\infty }([0,\infty ))$ topology.
$L^{\infty }([0,\infty ))$ topology.
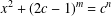 $x^{2}+(2c-1)^{m}=c^{n}$
$x^{2}+(2c-1)^{m}=c^{n}$
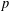 $p$-ADIC NUMBERS
$p$-ADIC NUMBERS
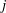 $j$-WISE RELATIVELY
$j$-WISE RELATIVELY  $r$-PRIME ALGEBRAIC INTEGERS
$r$-PRIME ALGEBRAIC INTEGERS
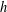 $h$-POLYNOMIALS OF CLUSTER SUBDIVISIONS HAVE ONLY REAL ZEROS
$h$-POLYNOMIALS OF CLUSTER SUBDIVISIONS HAVE ONLY REAL ZEROS
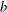 $b$-METRIC SPACES
$b$-METRIC SPACES