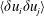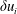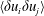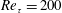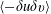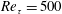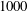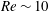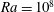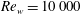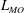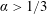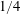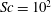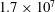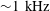Open access
Contents
JFM Papers
Structure function tensor equations in inhomogeneous turbulence
-
- Published online by Cambridge University Press:
- 25 June 2020, A5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reduced-order modelling of thick inertial flows around rotating cylinders
-
- Published online by Cambridge University Press:
- 24 June 2020, A1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
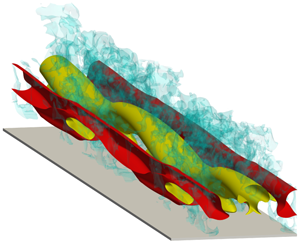
On the turbulence amplification in shock-wave/turbulent boundary layer interaction
-
- Published online by Cambridge University Press:
- 18 June 2020, A32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Flow organization and heat transfer in turbulent wall sheared thermal convection
-
- Published online by Cambridge University Press:
- 17 June 2020, A22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Artificial intelligence control of a turbulent jet
-
- Published online by Cambridge University Press:
- 17 June 2020, A27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Temperature-gradient-induced massive augmentation of solute dispersion in viscoelastic micro-flows
-
- Published online by Cambridge University Press:
- 16 June 2020, A23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transient convective spin-up dynamics
-
- Published online by Cambridge University Press:
- 16 June 2020, A24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the motion of slightly rarefied gas induced by a discontinuous surface temperature
-
- Published online by Cambridge University Press:
- 11 June 2020, A16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Oblique stripe solutions of channel flow
-
- Published online by Cambridge University Press:
- 09 June 2020, A7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fluid–structure stability analyses and nonlinear dynamics of flexible splitter plates interacting with a circular cylinder flow
-
- Published online by Cambridge University Press:
- 05 June 2020, A24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The circular capillary jump
-
- Published online by Cambridge University Press:
- 05 June 2020, A25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability of the solitary wave boundary layer subject to finite-amplitude disturbances
-
- Published online by Cambridge University Press:
- 02 June 2020, A20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Turbulence statistics in a negatively buoyant multiphase plume
-
- Published online by Cambridge University Press:
- 01 June 2020, A19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The viscous Holmboe instability for smooth shear and density profiles
-
- Published online by Cambridge University Press:
- 01 June 2020, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Solute transport and reaction in porous electrodes at high Schmidt numbers
-
- Published online by Cambridge University Press:
- 29 May 2020, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Response of the temporal turbulent boundary layer to decaying free-stream turbulence
-
- Published online by Cambridge University Press:
- 28 May 2020, A11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Theory of deep-water surface gravity waves derived from a Lagrangian
-
- Published online by Cambridge University Press:
- 27 May 2020, A7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
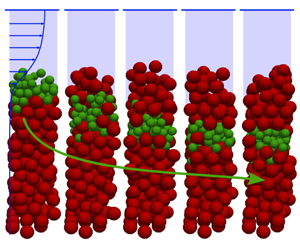
Discrete and continuum modelling of grain size segregation during bedload transport
-
- Published online by Cambridge University Press:
- 26 May 2020, A30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Flow dynamics and wall-pressure signatures in a high-Reynolds-number overexpanded nozzle with free shock separation
-
- Published online by Cambridge University Press:
- 26 May 2020, A29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Rapids
Acoustic excitation of Tollmien–Schlichting waves due to localised surface roughness
-
- Published online by Cambridge University Press:
- 21 May 2020, R5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation