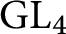 $ \operatorname {{\mathrm {GL}}}_4$
$ \operatorname {{\mathrm {GL}}}_4$
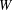 $W$-OPERATOR AND NONCROSSING PARTITIONS
$W$-OPERATOR AND NONCROSSING PARTITIONS
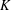 $K$ -THEORY OF GRASSMANNIANS
$K$ -THEORY OF GRASSMANNIANS
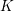 $K$ -theory of Grassmannians II: the Knutson–Vakil conjecture
$K$ -theory of Grassmannians II: the Knutson–Vakil conjecture