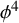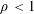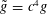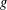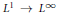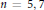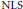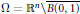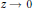Refine search
Actions for selected content:
22 results
The inverse scattering theory of Kadomtsev–Petviashvili II equations
- Part of
-
- Journal:
- Journal of Nonlinear Waves / Volume 1 / 2025
- Published online by Cambridge University Press:
- 04 August 2025, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quadratic Klein-Gordon equations with a potential in one dimension
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 11 July 2022, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON NONUNIQUENESS FOR THE ANISOTROPIC CALDERÓN PROBLEM WITH PARTIAL DATA
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 28 January 2020, e7
-
- Article
-
- You have access
- Open access
- Export citation
Generalizations of Menchov–Rademacher Theorem and Existence of Wave Operators in Schrödinger Evolution
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 20 December 2019, pp. 360-382
- Print publication:
- April 2021
-
- Article
- Export citation
On isotropic cloaking and interior transmission eigenvalue problems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 29 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 22 May 2017, pp. 253-280
-
- Article
- Export citation
On the Dispersive Estimate for the Dirichlet Schrödinger Propagator and Applications to Energy Critical NLS
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 5 / 01 October 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1110-1142
- Print publication:
- 01 October 2014
-
- Article
-
- You have access
- Export citation
Erratum to ‘Quantum Limits of Eisenstein Series and Scattering States’
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 4 / 01 December 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 827-828
- Print publication:
- 01 December 2013
-
- Article
-
- You have access
- Export citation
Quantum Limits of Eisenstein Series and Scattering States
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 4 / 01 December 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 814-826
- Print publication:
- 01 December 2013
-
- Article
-
- You have access
- Export citation
Résonances près de seuils d'opérateurs magnétiques de Pauli et de Dirac
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 5 / 01 October 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1095-1124
- Print publication:
- 01 October 2013
-
- Article
-
- You have access
- Export citation
Improved local energy decay for the wave equation on asymptotically Euclidean odd dimensional manifolds in the short range case
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 13 July 2012, pp. 635-650
- Print publication:
- July 2013
-
- Article
- Export citation
Low Frequency Estimates for Long Range Perturbations in Divergence Form
-
- Journal:
- Canadian Journal of Mathematics / Volume 63 / Issue 5 / 18 October 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 961-991
- Print publication:
- 18 October 2011
-
- Article
-
- You have access
- Export citation
An Optimized Perfectly Matched Layer for the Schrödinger Equation
-
- Journal:
- Communications in Computational Physics / Volume 9 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 20 August 2015, pp. 147-179
- Print publication:
- January 2011
-
- Article
- Export citation
Solvability conditions for some non-Fredholm operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 30 November 2010, pp. 249-271
-
- Article
-
- You have access
- Export citation
SEMICLASSICAL ANALYSIS FOR MAGNETIC SCATTERING BY TWO SOLENOIDAL FIELDS
-
- Journal:
- Journal of the London Mathematical Society / Volume 74 / Issue 3 / December 2006
- Published online by Cambridge University Press:
- 04 January 2007, pp. 695-716
- Print publication:
- December 2006
-
- Article
- Export citation
Partie imaginaire des résonances de Rayleigh dans le cas d'une boule
-
- Journal:
- Canadian Journal of Mathematics / Volume 58 / Issue 2 / 01 April 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 312-343
- Print publication:
- 01 April 2006
-
- Article
-
- You have access
- Export citation
Multiplicity of Resonances in Black Box Scattering
-
- Journal:
- Canadian Mathematical Bulletin / Volume 47 / Issue 3 / 01 September 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 407-416
- Print publication:
- 01 September 2004
-
- Article
-
- You have access
- Export citation
Semi-Classical Behavior of the Scattering Amplitude for Trapping Perturbations at Fixed Energy
-
- Journal:
- Canadian Journal of Mathematics / Volume 56 / Issue 4 / 01 August 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 794-824
- Print publication:
- 01 August 2004
-
- Article
-
- You have access
- Export citation
REGULARIZED TRACES AND TAYLOR EXPANSIONS FOR THE HEAT SEMIGROUP
-
- Journal:
- Journal of the London Mathematical Society / Volume 68 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 25 September 2003, pp. 402-418
- Print publication:
- October 2003
-
- Article
- Export citation
Eigenfunction Decay For the Neumann Laplacian on Horn-Like Domains
-
- Journal:
- Canadian Mathematical Bulletin / Volume 43 / Issue 1 / 01 March 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 51-59
- Print publication:
- 01 March 2000
-
- Article
-
- You have access
- Export citation
Corrigendum to “Spectral Theory for the Neumann Laplacian on Planar Domains with Horn-Like Ends”
-
- Journal:
- Canadian Journal of Mathematics / Volume 52 / Issue 1 / 01 February 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 119-122
- Print publication:
- 01 February 2000
-
- Article
-
- You have access
- Export citation