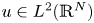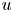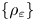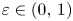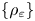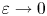Refine listing
Actions for selected content:
124 results in 49Jxx
On the Γ-limit of weighted fractional energies
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 December 2025, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Semi-discrete unbalanced optimal transport and quantization
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 17 October 2025, pp. 1-43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Travelling breather solutions in waveguides for cubic nonlinear Maxwell equations with retarded material laws
- Part of
-
- Journal:
- Journal of Nonlinear Waves / Volume 1 / 2025
- Published online by Cambridge University Press:
- 18 September 2025, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Existence of minimizers of the stability constant of Caffarelli–Kohn–Nirenberg inequality
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-23
-
- Article
- Export citation
Homogenization of vectorial free-discontinuity functionals with cohesive type surface terms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-71
-
- Article
- Export citation
On Bauschke–Bendit–Moursi modulus of averagedness and classifications of averaged nonexpansive operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sobolev spaces via chains in metric measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 04 August 2025, pp. 1-51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimization problems governed by systems of PDEs with uncertainties
- Part of
-
- Journal:
- Acta Numerica / Volume 34 / July 2025
- Published online by Cambridge University Press:
- 01 July 2025, pp. 491-577
-
- Article
-
- You have access
- Open access
- Export citation
Sobolev regularity of the inverse for minimizers of the neo-Hookean energy satisfying condition INV
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-21
-
- Article
- Export citation
Two relaxed inertial forward-backward-forward algorithms for solving monotone inclusions and an application to compressed sensing
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 13 January 2025, pp. 1-22
-
- Article
- Export citation
OPTIMAL CONTROL PROBLEMS GOVERNED BY MARGUERRE–VON KÁRMÁN EQUATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 01 January 2025, e38
-
- Article
- Export citation
On the existence of solutions to adversarial training in multiclass classification
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 03 December 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A singularly perturbed ruin problem for a two-dimensional Brownian motion in the positive quadrant
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 14 October 2024, pp. 269-283
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hilbert direct integrals of monotone operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 21 May 2024, pp. 1425-1456
- Print publication:
- August 2025
-
- Article
- Export citation
Sufficiency of
 $\boldsymbol{c}$-cyclical monotonicity in a class of multi-marginal optimal transport problems
$\boldsymbol{c}$-cyclical monotonicity in a class of multi-marginal optimal transport problems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 14 May 2024, pp. 68-81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Catenaries and minimal surfaces of revolution in hyperbolic space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp conditions for the validity of the Bourgain–Brezis–Mironescu formula
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1-24
-
- Article
- Export citation
On the lack of compactness in the axisymmetric neo-Hookean model
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 February 2024, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
From NeurODEs to AutoencODEs: A mean-field control framework for width-varying neural networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 08 February 2024, pp. 188-230
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topological regularity of isoperimetric sets in PI spaces having a deformation property
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 09 October 2023, pp. 611-633
- Print publication:
- April 2025
-
- Article
- Export citation