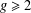Refine listing
Actions for selected content:
1073 results in 05Cxx
Disparity of clustering coefficients in the Holme‒Kim network model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 918-943
- Print publication:
- September 2018
-
- Article
- Export citation
Compound Poisson approximation of subgraph counts in stochastic block models with multiple edges
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 759-782
- Print publication:
- September 2018
-
- Article
- Export citation
Speeding up non-Markovian first-passage percolation with a few extra edges
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 858-886
- Print publication:
- September 2018
-
- Article
- Export citation
SYSTOLIC FILLINGS OF SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 28 August 2018, pp. 502-511
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
DETERMINING CROSSING NUMBERS OF GRAPHS OF ORDER SIX USING CYCLICPERMUTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 17 August 2018, pp. 353-362
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
GRAPH LABELLING TECHNIQUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 512-513
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
A STRUCTURED INVERSE SPECTRUM PROBLEM FOR INFINITE GRAPHS ANDUNBOUNDED OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 363-371
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Combinatorial Analysis of Growth Models for Series-Parallel Networks
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 14 August 2018, pp. 574-599
-
- Article
- Export citation
Exact Distance Colouring in Trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 24 July 2018, pp. 177-186
-
- Article
- Export citation
A GENERAL POSITION PROBLEM IN GRAPH THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 18 July 2018, pp. 177-187
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
Tilings in Randomly Perturbed Dense Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 16 July 2018, pp. 159-176
-
- Article
- Export citation
Turán Number of an Induced Complete Bipartite Graph Plus an Odd Cycle
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 16 July 2018, pp. 241-252
-
- Article
- Export citation
An Extremal Graph Problem with a Transcendental Solution
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 26 June 2018, pp. 303-324
-
- Article
- Export citation
Indistinguishable Sceneries on the Boolean Hypercube
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 05 June 2018, pp. 46-60
-
- Article
- Export citation
Spectral bounds in random graphs applied to spreading phenomena and percolation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 480-503
- Print publication:
- June 2018
-
- Article
- Export citation
Eigenvalue Ratios of Non-Negatively Curved Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 5 / September 2018
- Published online by Cambridge University Press:
- 23 May 2018, pp. 829-850
-
- Article
- Export citation
Generating Infinite Random Graphs
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 22 May 2018, pp. 847-868
-
- Article
- Export citation
On the Number of Solutions in Random Graph k-Colouring
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 21 May 2018, pp. 130-158
-
- Article
- Export citation
Volumes in the Uniform Infinite Planar Triangulation: From Skeletons to Generating Functions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 6 / November 2018
- Published online by Cambridge University Press:
- 21 May 2018, pp. 946-973
-
- Article
- Export citation
Random Recursive Trees and Preferential Attachment Trees are Random Split Trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 21 May 2018, pp. 81-99
-
- Article
- Export citation