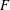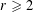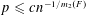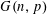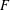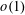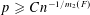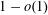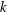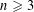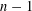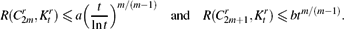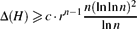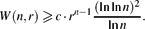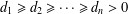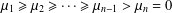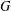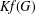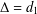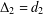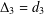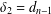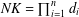Refine listing
Actions for selected content:
1073 results in 05Cxx
The Minimum Number of Edges in Uniform Hypergraphs with Property O
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 4 / July 2018
- Published online by Cambridge University Press:
- 19 December 2017, pp. 531-538
-
- Article
- Export citation
GENERALISATIONS OF THE DOYEN–WILSON THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 December 2017, pp. 166-167
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Stretch factor in a planar Poisson–Delaunay triangulation with a large intensity
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 35-56
- Print publication:
- March 2018
-
- Article
- Export citation
On the phase transition curve in a directed exponential random graph model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 272-301
- Print publication:
- March 2018
-
- Article
- Export citation
The probability of unusually large components in the near-critical Erdős–Rényi graph
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 245-271
- Print publication:
- March 2018
-
- Article
- Export citation
Jigsaw percolation on random hypergraphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 30 November 2017, pp. 1261-1277
- Print publication:
- December 2017
-
- Article
- Export citation
Phase transition in random distance graphs on the torus
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 30 November 2017, pp. 1278-1294
- Print publication:
- December 2017
-
- Article
- Export citation
Central limit theorem for the Horton–Strahler bifurcation ratio of general branch order
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 30 November 2017, pp. 1111-1124
- Print publication:
- December 2017
-
- Article
- Export citation
SYMMETRIC AND ASYMMETRIC RAMSEY PROPERTIES IN RANDOM HYPERGRAPHS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 23 November 2017, e28
-
- Article
-
- You have access
- Open access
- Export citation
ALTERNATING AND SYMMETRIC GROUPS WITH EULERIAN GENERATING GRAPH
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 10 November 2017, e24
-
- Article
-
- You have access
- Open access
- Export citation
Induced Turán Numbers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 2 / March 2018
- Published online by Cambridge University Press:
- 02 November 2017, pp. 274-288
-
- Article
- Export citation
New Classes of Degree Sequences with Fast Mixing Swap Markov Chain Sampling
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 2 / March 2018
- Published online by Cambridge University Press:
- 02 November 2017, pp. 186-207
-
- Article
- Export citation
ON THE COMPLEMENT OF THE ZERO-DIVISOR GRAPH OF A PARTIALLY ORDERED SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 02 November 2017, pp. 185-193
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
Linear Turán Numbers of Linear Cycles and Cycle-Complete Ramsey Numbers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 3 / May 2018
- Published online by Cambridge University Press:
- 02 November 2017, pp. 358-386
-
- Article
- Export citation
MAXIMUM GENUS EMBEDDINGS OF LATIN SQUARES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 495-504
-
- Article
-
- You have access
- Export citation
INTERPOLATED SCHUR MULTIPLE ZETA VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 25 October 2017, pp. 289-307
-
- Article
-
- You have access
- Export citation
On Edge-Disjoint Spanning Trees in a Randomly Weighted Complete Graph
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 2 / March 2018
- Published online by Cambridge University Press:
- 09 October 2017, pp. 228-244
-
- Article
- Export citation
Colourings of Uniform Hypergraphs with Large Girth and Applications
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 2 / March 2018
- Published online by Cambridge University Press:
- 09 October 2017, pp. 245-273
-
- Article
- Export citation
SOME NEW LOWER BOUNDS FOR THE KIRCHHOFF INDEX OF A GRAPH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 October 2017, pp. 1-10
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Bisections of Graphs Without Short Cycles
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 28 September 2017, pp. 44-59
-
- Article
- Export citation