Refine listing
Actions for selected content:
36 results in 13Bxx
LOCAL COHOMOLOGY OF MULTI-REES ALGEBRAS, JOINT REDUCTION NUMBERS AND PRODUCT OF COMPLETE IDEALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 228 / December 2017
- Published online by Cambridge University Press:
- 18 October 2016, pp. 1-20
- Print publication:
- December 2017
-
- Article
-
- You have access
- HTML
- Export citation
MULTIPLICITY AND ŁOJASIEWICZ EXPONENT OF GENERIC LINEAR SECTIONS OF MONOMIAL IDEALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 20 February 2015, pp. 191-201
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
On the family of affine threefolds
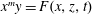 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}x^m y= F(x, z, t)$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}x^m y= F(x, z, t)$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 6 / June 2014
- Published online by Cambridge University Press:
- 09 June 2014, pp. 979-998
- Print publication:
- June 2014
-
- Article
- Export citation
Computation of Galois groups of rational polynomials
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 May 2014, pp. 141-158
-
- Article
-
- You have access
- Export citation
POLYNOMIAL EQUIVALENCE OF FINITE RINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 244-257
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
THE CLASSIFICATION OF COMMUTATIVE TORSION FILIAL RINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 18 July 2013, pp. 289-296
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Fibers of generic projections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 02 February 2010, pp. 435-456
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Oort groups and lifting problems
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 849-866
- Print publication:
- July 2008
-
- Article
-
- You have access
- Export citation
About directed unions of Artinian subrings of a Von Neumann regular ring
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 3 / December 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-304
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
The resultant and the Koszul complex of a set of forms
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 2 / December 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 348-356
- Print publication:
- December 1997
-
- Article
- Export citation
On complete integral closure and Archimedean valuation domains
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 3 / December 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 377-380
- Print publication:
- December 1996
-
- Article
-
- You have access
- Export citation
Pairs of rings with a bijective correspondence between the prime spectra
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 2 / October 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 238-245
- Print publication:
- October 1993
-
- Article
-
- You have access
- Export citation
Differential Completions and Differentially Simple Algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 3 / 01 September 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 314-319
- Print publication:
- 01 September 1989
-
- Article
-
- You have access
- Export citation
Permutation polynomials in several variables over residue class rings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 2 / October 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 171-175
- Print publication:
- October 1987
-
- Article
-
- You have access
- Export citation
Modules of generalized fractions
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 32-41
- Print publication:
- June 1982
-
- Article
- Export citation
A note on involutary division algebras of the second kind
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 34-36
- Print publication:
- June 1977
-
- Article
- Export citation
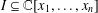
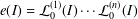
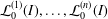
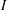
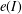
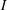
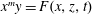
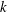
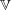
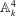
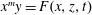
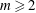
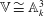
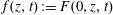
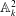
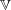
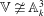
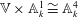
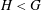
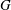
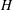
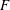
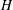
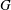
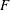
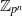
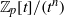
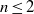
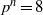
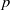
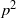
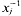 of degree - 1 be a formal inverse of
of degree - 1 be a formal inverse of 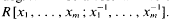 In [2, §2] we introduced a graded complex of
In [2, §2] we introduced a graded complex of