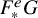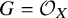Refine listing
Actions for selected content:
158 results in 13Dxx
High Frobenius pushforwards generate the bounded derived category
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 14 / 2026
- Published online by Cambridge University Press:
- 21 January 2026, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Koszul binomial edge ideals
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 14 / 2026
- Published online by Cambridge University Press:
- 09 January 2026, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POWERS OF FACET IDEALS OF SIMPLICIAL TREES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 261 / 2026
- Published online by Cambridge University Press:
- 18 December 2025, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Intersection Theorem for DG-modules over non-positive DG-rings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 12 December 2025, pp. 1-18
-
- Article
- Export citation
A new hierarchy for complex plane curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 12 November 2025, pp. 1-25
-
- Article
- Export citation
On the relevant domain of the Hilbert function of a finite multiprojective scheme
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-31
-
- Article
- Export citation
Silting, cosilting and extensions of commutative rings
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 27 October 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hartshorne’s question on cofiniteness of complexes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 07 October 2025, pp. 1-14
-
- Article
- Export citation
Regularity and multiplicity of Veronese type algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 69 / Issue 1 / March 2026
- Published online by Cambridge University Press:
- 08 August 2025, pp. 150-178
- Print publication:
- March 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
G-dimensions for DG-modules over commutative DG-rings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 01 August 2025, pp. 1370-1389
-
- Article
- Export citation
ON THE REGULARITY INDEX OF FAT POINTS WHOSE SUPPORT IS CONTAINED IN A LINEAR PROPER SUBSPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 113 / Issue 1 / February 2026
- Published online by Cambridge University Press:
- 20 June 2025, pp. 90-97
- Print publication:
- February 2026
-
- Article
- Export citation
Homological full-and-faithfulness of comodule inclusion and contramodule forgetful functors
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 21 May 2025, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Derived functors and Hilbert polynomials over hypersurface rings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 02 April 2025, pp. 898-908
-
- Article
- Export citation
Linear syzygies of curves in weighted projective space
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 15 August 2025, pp. 916-944
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bernstein–Sato polynomials of locally quasi-homogeneous divisors in
 $\mathbb{C}^{3}$
$\mathbb{C}^{3}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 20 August 2025, pp. 859-915
- Print publication:
- April 2025
-
- Article
- Export citation
Koszul homomorphisms and universal resolutions in local algebra
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 March 2025, e63
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The cokernel of a polynomial push-forward of a random integral matrix with concentrated residue
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 229-257
- Print publication:
- March 2025
-
- Article
- Export citation
ON THE ASYMPTOTIC BEHAVIOR OF THE VASCONCELOS INVARIANT FOR GRADED MODULES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 296-310
-
- Article
- Export citation
Deformations of morphisms of sheaves
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 04 February 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LOCAL COHOMOLOGY UNDER SMALL PERTURBATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 183-200
-
- Article
- Export citation