Refine listing
Actions for selected content:
103 results in 13Fxx
CLUSTER STRUCTURES ON HIGHER TEICHMULLER SPACES FOR CLASSICAL GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 08 May 2019, e13
-
- Article
-
- You have access
- Open access
- Export citation
ON THE ARITHMETIC OF MORI MONOIDS AND DOMAINS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 08 April 2019, pp. 313-322
- Print publication:
- May 2020
-
- Article
-
- You have access
- Export citation
LINEAR QUOTIENTS AND MULTIGRADED SHIFTS OF BOREL IDEALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 48-57
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Pólya S3-extensions of ℚ
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1421-1433
- Print publication:
- December 2019
-
- Article
- Export citation
Newton Complementary Duals of
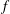 $f$-Ideals
$f$-Ideals
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 15 October 2018, pp. 231-241
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
On the General Solution of the Heideman–Hogan Family of Recurrences
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 14 August 2018, pp. 1113-1125
-
- Article
- Export citation
A CONJECTURE ON
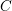 $C$-MATRICES OF CLUSTER ALGEBRAS
$C$-MATRICES OF CLUSTER ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 238 / June 2020
- Published online by Cambridge University Press:
- 19 June 2018, pp. 37-46
- Print publication:
- June 2020
-
- Article
-
- You have access
- HTML
- Export citation
Cluster algebras and continued fractions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 3 / March 2018
- Published online by Cambridge University Press:
- 22 December 2017, pp. 565-593
- Print publication:
- March 2018
-
- Article
- Export citation
CANONICAL LIFTS OF FAMILIES OFELLIPTIC CURVES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 233 / March 2019
- Published online by Cambridge University Press:
- 02 November 2017, pp. 193-213
- Print publication:
- March 2019
-
- Article
-
- You have access
- HTML
- Export citation
FACTORIZATION IN PRÜFER DOMAINS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 401-409
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
Zero cycles with modulus and zero cycles on singular varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 09 October 2017, pp. 120-187
- Print publication:
- January 2018
-
- Article
- Export citation
HYPERBOLIC 3-MANIFOLDS AND CLUSTER ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 235 / September 2019
- Published online by Cambridge University Press:
- 28 September 2017, pp. 1-25
- Print publication:
- September 2019
-
- Article
-
- You have access
- HTML
- Export citation
QUANTISATION SPACES OF CLUSTER ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 04 September 2017, pp. 273-284
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
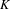 $K$-THEORY OF MONOID ALGEBRAS AND A QUESTIONOF GUBELADZE
$K$-THEORY OF MONOID ALGEBRAS AND A QUESTIONOF GUBELADZE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 10 August 2017, pp. 1051-1085
- Print publication:
- September 2019
-
- Article
- Export citation
LYUBEZNIK NUMBERS OF LOCAL RINGS AND LINEAR STRANDS OF GRADED IDEALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 231 / September 2018
- Published online by Cambridge University Press:
- 10 May 2017, pp. 23-54
- Print publication:
- September 2018
-
- Article
-
- You have access
- HTML
- Export citation
Theta bases are atomic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 6 / June 2017
- Published online by Cambridge University Press:
- 26 April 2017, pp. 1217-1219
- Print publication:
- June 2017
-
- Article
- Export citation
THE PROJECTIVE DIMENSION OF THE EDGE IDEAL OF A VERY WELL-COVERED GRAPH
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 12 April 2017, pp. 160-179
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
ASYMPTOTIC TRIANGULATIONS AND COXETER TRANSFORMATIONS OF THE ANNULUS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 27 February 2017, pp. 63-96
- Print publication:
- January 2018
-
- Article
-
- You have access
- Export citation
Defining Coarsenings of Valuations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 10 January 2017, pp. 665-687
-
- Article
- Export citation
A DESCENT THEOREM FOR FORMAL SMOOTHNESS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 229 / March 2018
- Published online by Cambridge University Press:
- 08 December 2016, pp. 113-140
- Print publication:
- March 2018
-
- Article
-
- You have access
- HTML
- Export citation
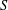
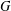
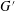
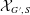
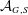
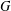
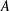
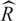
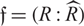
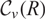
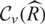
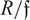
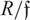
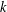
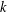
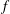
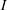
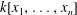
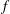
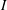
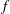
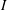
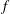
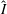
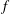
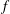
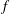
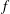
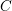
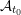
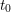
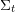
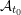
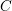

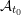
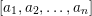
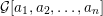
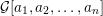
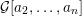
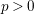
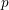
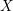
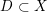
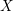
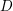
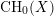
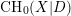
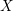
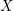
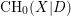
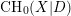
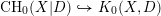
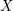
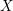
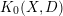
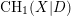
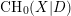
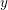
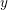
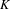
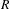
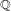
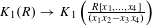
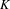
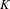
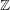
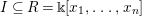
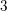
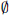 -definable (non-trivial) Henselian valuations. We then draw some Galois-theoretic conclusions from our results.
-definable (non-trivial) Henselian valuations. We then draw some Galois-theoretic conclusions from our results.