Refine listing
Actions for selected content:
103 results in 13Fxx
Symbolic Powers of Monomial Ideals
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 13 June 2016, pp. 39-55
-
- Article
- Export citation
Irreducible decomposition of binomial ideals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 1319-1332
- Print publication:
- June 2016
-
- Article
- Export citation
Elasticity in Polynomial-Type Extensions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 28 March 2016, pp. 581-590
-
- Article
- Export citation
Application of Braiding Sequences. II. Polynomial Invariants of Positive Knots
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 1037-1064
-
- Article
- Export citation
Upper semi-continuity of the Hilbert–Kunz multiplicity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 3 / March 2016
- Published online by Cambridge University Press:
- 02 February 2016, pp. 477-488
- Print publication:
- March 2016
-
- Article
- Export citation
EXPLICIT CONSTRUCTION OF COMPANION BASES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 357-384
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
ON THE WEAK GROTHENDIECK GROUP OF A BEZOUT RING
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 617-635
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
Generalized friezes and a modified Caldero–Chapoton map depending on a rigid object
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 218 / June 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 101-124
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Purity for graded potentials and quantum cluster positivity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 10 / October 2015
- Published online by Cambridge University Press:
- 19 May 2015, pp. 1913-1944
- Print publication:
- October 2015
-
- Article
- Export citation
Linear difference equations, frieze patterns, and the combinatorial Gale transform
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 22 August 2014, e22
-
- Article
-
- You have access
- Open access
- Export citation
A vanishing theorem and symbolic powers of planar point ideals
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 October 2013, pp. 373-387
-
- Article
-
- You have access
- Export citation
Linear independence of cluster monomials for skew-symmetric cluster algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 10 / October 2013
- Published online by Cambridge University Press:
- 28 August 2013, pp. 1753-1764
- Print publication:
- October 2013
-
- Article
- Export citation
Bases for cluster algebras from surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 2 / February 2013
- Published online by Cambridge University Press:
- 07 December 2012, pp. 217-263
- Print publication:
- February 2013
-
- Article
- Export citation
Quivers with potentials associated to triangulated surfaces, Part III: tagged triangulations and cluster monomials
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 01 November 2012, pp. 1833-1866
- Print publication:
- November 2012
-
- Article
-
- You have access
- Export citation
Proof of a positivity conjecture of M. Kontsevich on non-commutative cluster variables
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 31 October 2012, pp. 1821-1832
- Print publication:
- November 2012
-
- Article
-
- You have access
- Export citation
Gorenstein rings through face rings of manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 4 / July 2009
- Published online by Cambridge University Press:
- 01 July 2009, pp. 993-1000
- Print publication:
- July 2009
-
- Article
-
- You have access
- Export citation
STRONGLY IRREDUCIBLE IDEALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 145-154
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
On The Asymptotic Values of Length Functions In Krull And Finitely Generated commutative Monoids
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 3 / June 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 421-436
- Print publication:
- June 2003
-
- Article
-
- You have access
- Export citation
Prüfer domains and pure submodules of direct sums of ideals
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 425-432
- Print publication:
- December 1999
-
- Article
- Export citation
Commutative rings with comparable regular elements
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 1 / February 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 90-108
- Print publication:
- February 1996
-
- Article
-
- You have access
- Export citation
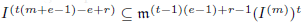 for all positive integers
for all positive integers 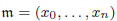 . This captures two conjectures (
. This captures two conjectures (
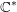
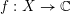
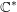
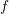
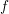
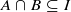 implies that either
implies that either 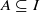 or
or 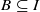 . In this paper we study strongly irreducible ideals in different rings. The relations between strongly irreducible ideals of a ring and strongly irreducible ideals of localizations of the ring are also studied. Furthermore, a topology similar to the Zariski topology related to strongly irreducible ideals is introduced. This topology has the Zariski topology defined by prime ideals as one of its subspace topologies.
. In this paper we study strongly irreducible ideals in different rings. The relations between strongly irreducible ideals of a ring and strongly irreducible ideals of localizations of the ring are also studied. Furthermore, a topology similar to the Zariski topology related to strongly irreducible ideals is introduced. This topology has the Zariski topology defined by prime ideals as one of its subspace topologies.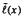 and
and 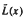 on
on 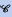 be the class of commutative rings
be the class of commutative rings 