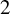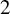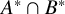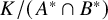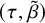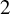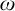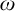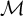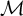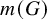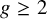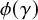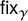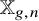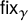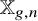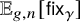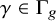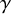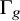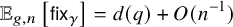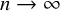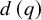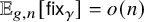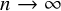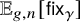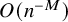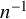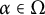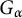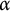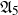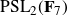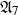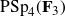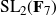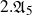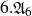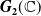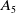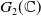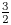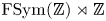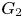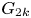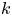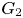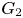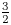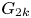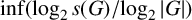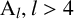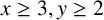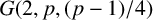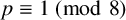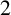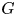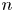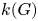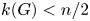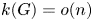Refine listing
Actions for selected content:
147 results in 20Bxx
A BOREL MAXIMAL COFINITARY GROUP
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 11 December 2023, pp. 808-821
- Print publication:
- June 2025
-
- Article
- Export citation
A question of Frohardt on
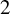 $2$-groups, skew translation quadrangles of even order and cyclic STGQs
$2$-groups, skew translation quadrangles of even order and cyclic STGQs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 06 December 2023, e109
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A lattice theoretical interpretation of generalized deep holes of the Leech lattice vertex operator algebra
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 27 September 2023, e86
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CLASSIFICATION OF
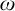 $\omega $-CATEGORICAL MONADICALLY STABLE STRUCTURES
$\omega $-CATEGORICAL MONADICALLY STABLE STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 19 September 2023, pp. 460-495
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CAYLEY GRAPHS AND GRAPHICAL REGULAR REPRESENTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 15 September 2023, pp. 161-162
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
The maximal size of a minimal generating set
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 10 August 2023, e70
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Asymptotic Statistics of Random Covering Surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 15 May 2023, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Jordan–Hölder theorem for skew left braces and their applications to multipermutation solutions of the Yang–Baxter equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 24 April 2023, pp. 793-809
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONSTRUCTING MAXIMAL COFINITARY GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 251 / September 2023
- Published online by Cambridge University Press:
- 30 January 2023, pp. 622-651
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite transitive groups having many suborbits of cardinality at most 2 and an application to the enumeration of Cayley graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 30 January 2023, pp. 345-366
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite quasisimple groups acting on rationally connected threefolds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 06 December 2022, pp. 531-568
- Print publication:
- May 2023
-
- Article
- Export citation
Products of derangements in simple permutation groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 23 September 2022, e83
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON 2-TRANSITIVE SETS OF EQUIANGULAR LINES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 22 August 2022, pp. 134-145
- Print publication:
- February 2023
-
- Article
- Export citation
Polyhedral groups in
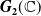 $\textbf{G}_{\textbf{2}}(\mathbb C)$
$\textbf{G}_{\textbf{2}}(\mathbb C)$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 11 August 2022, pp. S123-S128
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE AUTOMORPHISM GROUP OF THE FRAÏSSÉ LIMIT OF FINITE HEYTING ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 07 June 2022, pp. 1310-1320
- Print publication:
- September 2023
-
- Article
- Export citation
ON THE CAYLEYNESS OF PRAEGER–XU GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 11 May 2022, pp. 353-356
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the spread of infinite groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 214-228
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE NUMBER OF SET ORBITS OF PERMUTATION GROUPS AND THE GROUP ORDER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 27 January 2022, pp. 89-101
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITE TWO-DISTANCE-TRANSITIVE DIHEDRANTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 26 January 2022, pp. 386-401
- Print publication:
- December 2022
-
- Article
- Export citation
On the number of conjugacy classes of a primitive permutation group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 13 December 2021, pp. 115-136
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation