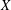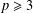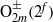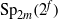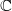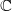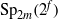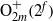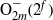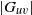Refine listing
Actions for selected content:
147 results in 20Bxx
ON GRAPHS OF PRIME VALENCY ADMITTING A SOLVABLE ARC-TRANSITIVE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 13 May 2015, pp. 214-227
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
Champ: a Cherednik algebra Magma package
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 April 2015, pp. 266-307
-
- Article
-
- You have access
- Export citation
 $\wedge$-TRANSITIVE DIGRAPHS PRESERVING A CARTESIAN DECOMPOSITION
$\wedge$-TRANSITIVE DIGRAPHS PRESERVING A CARTESIAN DECOMPOSITION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 31 March 2015, pp. 85-107
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
ON REGULAR SUBGROUPS OF THE AFFINE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 08 October 2014, pp. 76-85
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
Computing symmetry groups of polyhedra
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 October 2014, pp. 565-581
-
- Article
-
- You have access
- Export citation
FINITE 3-GEODESIC TRANSITIVE BUT NOT 3-ARC TRANSITIVE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 23 September 2014, pp. 183-190
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
FINITE
 $s$-GEODESIC TRANSITIVE GRAPHS
$s$-GEODESIC TRANSITIVE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 27 November 2013, pp. 175-176
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
A REMARK ON THE PERMUTATION REPRESENTATIONS AFFORDED BY THE EMBEDDINGS OF
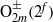 ${ \text{O} }_{2m}^{\pm } ({2}^{f} )$ IN
${ \text{O} }_{2m}^{\pm } ({2}^{f} )$ IN 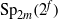 ${\text{Sp} }_{2m} ({2}^{f} )$
${\text{Sp} }_{2m} ({2}^{f} )$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 19 September 2013, pp. 331-336
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
A NOTE ON THE WEISS CONJECTURE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 07 August 2013, pp. 356-361
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
PRIMITIVE PERMUTATION GROUPS CONTAINING A CYCLE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 18 July 2013, pp. 159-165
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
ON THE ORDER OF ARC-STABILISERS IN ARC-TRANSITIVE GRAPHS, II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 02 August 2012, pp. 441-447
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Computing Hall subgroups of finite groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 August 2012, pp. 205-218
-
- Article
-
- You have access
- Export citation
TRIPLE FACTORISATIONS: GROUP THEORETIC AND GEOMETRIC APPROACHES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 27 March 2012, pp. 521-524
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
EMBEDDING PERMUTATION GROUPS INTO WREATH PRODUCTS IN PRODUCT ACTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 24 April 2012, pp. 127-136
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
LOCALLY PRIMITIVE GRAPHS AND BIDIRECT PRODUCTS OF GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 14 October 2011, pp. 231-242
- Print publication:
- October 2011
-
- Article
-
- You have access
- Export citation
ON MINIMAL DEGREES OF PERMUTATION REPRESENTATIONS OF ABELIAN QUOTIENTS OF FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 28 September 2011, pp. 408-413
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
Searching for small simple automorphic loops
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 August 2011, pp. 200-213
-
- Article
-
- You have access
- Export citation
TETRAVALENT ARC-TRANSITIVE GRAPHS WITH UNBOUNDED VERTEX-STABILIZERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 15 March 2011, pp. 79-89
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
Cubic graphs admitting transitive non-abelian characteristically simple groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 19 January 2011, pp. 113-123
-
- Article
-
- You have access
- Export citation
ON COMMON DIVISORS OF MULTINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 13 October 2010, pp. 138-157
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation