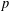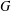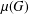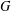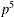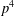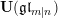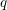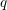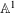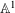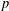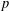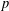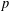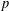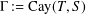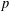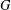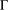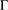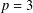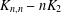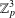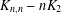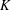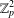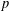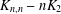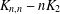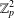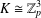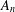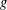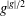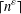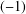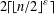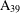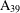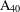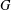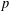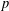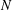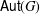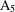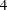Refine listing
Actions for selected content:
147 results in 20Bxx
A generalisation of von Staudt’s theorem on cross-ratios
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 168 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 22 February 2019, pp. 601-612
- Print publication:
- May 2020
-
- Article
-
- You have access
- Export citation
ALGEBRAIC MODELS OF LARGE SCALE GENOME REARRANGEMENT EVENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 29 January 2019, pp. 338-339
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Galois theory for general systems of polynomial equations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 2 / February 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 229-245
- Print publication:
- February 2019
-
- Article
- Export citation
MINIMAL EXCEPTIONAL
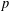 $p$ -GROUPS
$p$ -GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 434-438
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
MULTIPLICATION FORMULAS AND SEMISIMPLICITY FOR
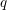 $q$-SCHUR SUPERALGEBRAS
$q$-SCHUR SUPERALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 237 / March 2020
- Published online by Cambridge University Press:
- 30 April 2018, pp. 98-126
- Print publication:
- March 2020
-
- Article
-
- You have access
- HTML
- Export citation
RIGID LOCAL SYSTEMS ON
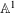 $\mathbb{A}^{1}$ WITH FINITE MONODROMY
$\mathbb{A}^{1}$ WITH FINITE MONODROMY
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 785-846
- Print publication:
- 2018
-
- Article
- Export citation
ALTERNATING AND SYMMETRIC GROUPS WITH EULERIAN GENERATING GRAPH
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 10 November 2017, e24
-
- Article
-
- You have access
- Open access
- Export citation
SIMPLE GROUPS, PRODUCT ACTIONS, AND GENERALIZED QUADRANGLES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 234 / June 2019
- Published online by Cambridge University Press:
- 14 September 2017, pp. 87-126
- Print publication:
- June 2019
-
- Article
-
- You have access
- HTML
- Export citation
THE TWO-ARC-TRANSITIVE GRAPHS OF SQUARE-FREE ORDER ADMITTING ALTERNATING OR SYMMETRIC GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 29 March 2017, pp. 127-144
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
SOME INFINITE PERMUTATION GROUPS AND RELATED FINITE LINEAR GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 25 October 2016, pp. 136-149
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
A Switch Function-Based Gas-Kinetic Scheme for Simulation of Inviscid and Viscous Compressible Flows
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 08 July 2016, pp. 703-721
- Print publication:
- October 2016
-
- Article
- Export citation
Finding 47:23 in the Baby Monster
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 June 2016, pp. 229-234
-
- Article
-
- You have access
- Export citation
FINITE NORMAL 2-GEODESIC TRANSITIVE CAYLEY GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 338-348
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
2-ARC-TRANSITIVE REGULAR COVERS OF
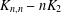 $K_{n,n}-nK_{2}$ HAVING THE COVERING TRANSFORMATION GROUP
$K_{n,n}-nK_{2}$ HAVING THE COVERING TRANSFORMATION GROUP 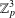 $\mathbb{Z}_{p}^{3}$
$\mathbb{Z}_{p}^{3}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 145-170
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
ON ARC-REGULAR FROBENIUS METACIRCULANTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 10 February 2016, pp. 20-29
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
FINDING INVOLUTIONS WITH SMALL SUPPORT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 11 January 2016, pp. 43-47
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
A 2-ARC TRANSITIVE PENTAVALENT CAYLEY GRAPH OF
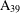 $\text{A}_{39}$
$\text{A}_{39}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 January 2016, pp. 441-446
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
RELATIVE ELEMENTARY ABELIAN GROUPS AND A CLASS OF EDGE-TRANSITIVE CAYLEY GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 20 November 2015, pp. 241-251
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
AUTOMORPHISM GROUPS OF SELF-COMPLEMENTARY VERTEX-TRANSITIVE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 238-247
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
THE CONTRIBUTION OF L. G. KOVÁCS TO THE THEORY OF PERMUTATION GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 05 November 2015, pp. 20-33
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation