Refine listing
Actions for selected content:
147 results in 20Bxx
Constructions for arc-transitive digraphs
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 1 / August 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 61-80
- Print publication:
- August 1995
-
- Article
-
- You have access
- Export citation
Inherited group actions on ℝ-trees
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 206-213
- Print publication:
- June 1995
-
- Article
- Export citation
Some examples of groups with no non-trivial action on a Λ-tree
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 214-219
- Print publication:
- June 1995
-
- Article
- Export citation
Balanced directed cycle designs based on cyclic groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 2 / April 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 210-218
- Print publication:
- April 1995
-
- Article
-
- You have access
- Export citation
Kronecker classes of fields and covering subgroups of finite groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 1 / August 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 17-34
- Print publication:
- August 1994
-
- Article
-
- You have access
- Export citation
Vertex-primitive half-transitive graphs
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 1 / August 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 113-124
- Print publication:
- August 1994
-
- Article
-
- You have access
- Export citation
Vertex-transitive graphs which are not Cayley graphs, I
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 1 / February 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 53-63
- Print publication:
- February 1994
-
- Article
-
- You have access
- Export citation
Maximal subgroups of infinite dimensional general linear groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 3 / December 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 338-351
- Print publication:
- December 1992
-
- Article
-
- You have access
- Export citation
Goldie M-groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 2 / October 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 237-246
- Print publication:
- October 1991
-
- Article
-
- You have access
- Export citation
Rigidity of Decomposition laws and number fields
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 2 / October 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 171-186
- Print publication:
- October 1991
-
- Article
-
- You have access
- Export citation
Kronecker classes of field extensions of small degree
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 2 / April 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-315
- Print publication:
- April 1991
-
- Article
-
- You have access
- Export citation
Collineation groups preserving an oval in a projective place of odd order
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 1 / February 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 156-170
- Print publication:
- February 1990
-
- Article
-
- You have access
- Export citation
Primitive permutation groups with a doubly transitive subconstituent
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 1 / August 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 66-77
- Print publication:
- August 1988
-
- Article
-
- You have access
- Export citation
On the O'Nan-Scott theorem for finite primitive permutation groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 3 / June 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 389-396
- Print publication:
- June 1988
-
- Article
-
- You have access
- Export citation
Chief Series and Right Regular Representations of Finite p-Groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 2 / April 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 225-232
- Print publication:
- April 1988
-
- Article
-
- You have access
- Export citation
A note on generalised wreath product groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 3 / December 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 415-420
- Print publication:
- December 1985
-
- Article
-
- You have access
- Export citation
Multipliers of Banach valued function spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 1 / August 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 51-62
- Print publication:
- August 1985
-
- Article
-
- You have access
- Export citation
The structure of a group of permutation polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 2 / April 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 164-170
- Print publication:
- April 1985
-
- Article
-
- You have access
- Export citation
On transitive permutation groups with a subgroup satisfying a certain conjugacy condition
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 1 / February 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 69-86
- Print publication:
- February 1984
-
- Article
-
- You have access
- Export citation
Attaching graphs to pseudo-similar vertices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 1 / February 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 53-58
- Print publication:
- February 1984
-
- Article
-
- You have access
- Export citation
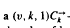 -design, is a decomposition of the complete directed graph
-design, is a decomposition of the complete directed graph 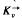 into edge disjoint directed cycles of length
into edge disjoint directed cycles of length 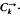 -designs admitting the holomorph {ø
-designs admitting the holomorph {ø