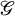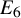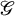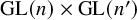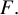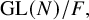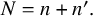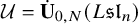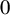Refine listing
Actions for selected content:
279 results in 20Gxx
Picky elements, subnormalisers, and character correspondences
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 30 September 2025, e161
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The stack of G-zips is a Mori dream space
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 19 September 2025, pp. 1-36
-
- Article
- Export citation
BUBBLES IN THE AFFINE BRAUER AND KAUFFMAN CATEGORIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 September 2025, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On G2-manifolds and geometry in dimensions 6 and 8
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 12 August 2025, pp. 1-9
-
- Article
- Export citation
Contramodules for algebraic groups: the existence of mock projectives
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 04 August 2025, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Smooth locus of twisted affine Schubert varieties and twisted affine Demazure modules
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 18 July 2025, e121
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Morava J-invariant
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 02 July 2025, e104
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Moments, Exponential Sums, and Monodromy Groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 June 2025, e101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Eisenstein Cohomology for
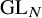 $\mathrm {GL}_N$ and the special values of Rankin–Selberg L-functions over a totally imaginary number field
$\mathrm {GL}_N$ and the special values of Rankin–Selberg L-functions over a totally imaginary number field
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e86
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $\mathbf {5 \times 5}$-graded Lie algebras, cubic norm structures and quadrangular algebras
$\mathbf {5 \times 5}$-graded Lie algebras, cubic norm structures and quadrangular algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e88
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Polishchuk’s conjecture and Kazhdan–Laumon representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 26 August 2025, pp. 993-1020
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A tensor restriction theorem over finite fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 29 August 2025, pp. 1021-1053
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A categorical action of the shifted
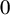 $0$-affine algebra
$0$-affine algebra
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 15 April 2025, e74
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Semisimple random walks on the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 03 March 2025, pp. 3090-3147
- Print publication:
- October 2025
-
- Article
- Export citation
Generalised Temperley–Lieb algebras of type G(r, p, n)
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 08 April 2025, pp. 193-227
- Print publication:
- March 2025
-
- Article
- Export citation
An Iwahori theoretic mod
 $p$ local Langlands correspondence
$p$ local Langlands correspondence
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 17 February 2025, pp. 805-817
- Print publication:
- September 2025
-
- Article
- Export citation
THE COHOMOLOGY OF p-ADIC DELIGNE-LUSZTIG SCHEMES OF COXETER TYPE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1429-1462
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Closed approximate subgroups: compactness, amenability and approximate lattices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 January 2025, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Ekedahl–Oort stratification and the semi-module stratification
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 January 2025, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Oriented Temperley–Lieb algebras and combinatorial Kazhdan–Lusztig theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 January 2025, pp. 1-43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation