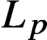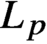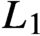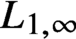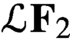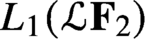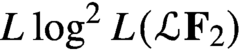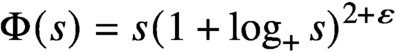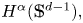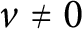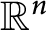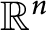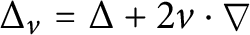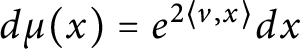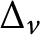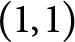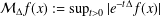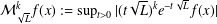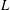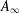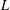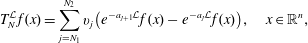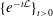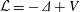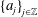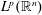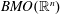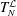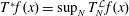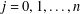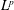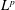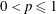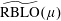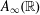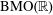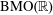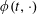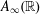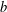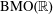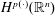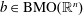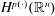Refine listing
Actions for selected content:
271 results in 42Bxx
Noncommutative strong maximals and almost uniform convergence in several directions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 November 2020, e57
-
- Article
-
- You have access
- Open access
- Export citation
The Fourier extension operator of distributions in Sobolev spaces of the sphere and the Helmholtz equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 16 November 2020, pp. 1768-1789
- Print publication:
- December 2021
-
- Article
- Export citation
A revisit on the compactness of commutators
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 20 August 2020, pp. 1667-1697
- Print publication:
- December 2021
-
- Article
- Export citation
Sharp endpoint estimates for some operators associated with the Laplacian with drift in Euclidean space
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 16 June 2020, pp. 1278-1304
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
Edge corrections for parallel-plate capacitors
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 30 April 2020, pp. 226-241
-
- Article
-
- You have access
- Open access
- Export citation
BOUNDEDNESS OF MAXIMAL FUNCTIONS ON NONDOUBLING PARABOLIC MANIFOLDS WITH ENDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 11 March 2020, pp. 320-344
- Print publication:
- December 2021
-
- Article
- Export citation
On Restriction Estimates for the Zero Radius Sphere over Finite Fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 27 February 2020, pp. 769-786
- Print publication:
- June 2021
-
- Article
- Export citation
WEIGHTED BESOV AND TRIEBEL–LIZORKIN SPACES ASSOCIATED WITH OPERATORS AND APPLICATIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 26 February 2020, e11
-
- Article
-
- You have access
- Open access
- Export citation
Boundedness of Differential Transforms for Heat Semigroups Generated by Schrödinger Operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 12 February 2020, pp. 622-655
- Print publication:
- June 2021
-
- Article
- Export citation
Maximal functions associated with families of homogeneous curves: Lp bounds for P ≤ 2
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 03 February 2020, pp. 398-412
-
- Article
- Export citation
Bilinear identities involving the k-plane transform and Fourier extension operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 27 January 2020, pp. 3349-3377
- Print publication:
- December 2020
-
- Article
- Export citation
FACTORIZING MULTILINEAR KERNEL OPERATORS THROUGH SPACES OF VECTOR MEASURES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 13 January 2020, pp. 30-51
- Print publication:
- February 2022
-
- Article
- Export citation
BOCHNER–RIESZ MEANS ON BLOCK-SOBOLEV SPACES IN COMPACT LIE GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 176-192
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Sharp Bounds for Oscillatory Integral Operators with Homogeneous Polynomial Phases
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 20 December 2019, pp. 771-786
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Block Decomposition and Weighted Hausdorff Content
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 16 December 2019, pp. 141-156
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
The John–Nirenberg Inequality for the Regularized BLO Space on Non-homogeneous Metric Measure Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 10 December 2019, pp. 643-654
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
FLOW WITH
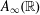 $A_{\infty }(\mathbb{R})$ DENSITY AND TRANSPORT EQUATION IN
$A_{\infty }(\mathbb{R})$ DENSITY AND TRANSPORT EQUATION IN 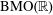 $\text{BMO}(\mathbb{R})$
$\text{BMO}(\mathbb{R})$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 29 November 2019, e43
-
- Article
-
- You have access
- Open access
- Export citation
A unified method for maximal truncated Calderón–Zygmund operators in general function spaces by sparse domination
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 22 November 2019, pp. 229-247
-
- Article
- Export citation
FKN theorem for the multislice, with applications
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 18 October 2019, pp. 200-212
-
- Article
- Export citation
Discrete Paraproduct Operators on Variable Hardy Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 04 October 2019, pp. 304-317
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation