Refine listing
Actions for selected content:
271 results in 42Bxx
A PARABOLIC SINGULAR INTEGRAL OPERATOR WITH ROUGH KERNEL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 163-179
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
MIXED NORM ESTIMATES FOR POTENTIAL OPERATORS RELATED TO THE RADON TRANSFORM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 181-191
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
Multidimensional Hausdorff operators on the real Hardy space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 1 / August 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 79-86
- Print publication:
- August 2007
-
- Article
-
- You have access
- Export citation
Estimates for kernels of intertwining operators on SL(n, R)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 1 / August 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 105-120
- Print publication:
- August 2006
-
- Article
-
- You have access
- Export citation
Some new Besov and Triebel-Lizorkin spaces associated with para-accretive functions on spaces of homogeneous type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 2 / April 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 229-262
- Print publication:
- April 2006
-
- Article
-
- You have access
- Export citation
Maximal transference and summability of multilinear Fourier series
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 1 / February 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 65-80
- Print publication:
- February 2006
-
- Article
-
- You have access
- Export citation
Composite Cosine Transforms
- Part of
-
- Journal:
- Mathematika / Volume 52 / Issue 1-2 / December 2005
- Published online by Cambridge University Press:
- 21 December 2009, pp. 53-68
- Print publication:
- December 2005
-
- Article
- Export citation
Local hardy and BMO spaces on non-homogeneous spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 2 / October 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-182
- Print publication:
- October 2005
-
- Article
-
- You have access
- Export citation
Two weight norm inequalities for communtators of one-sided singular integrals and the one-sided discrete square function
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 1 / August 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 77-94
- Print publication:
- August 2005
-
- Article
-
- You have access
- Export citation
The higher order commutators of the fractional integrals on Hardy spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 1 / August 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 11-24
- Print publication:
- August 2005
-
- Article
-
- You have access
- Export citation
Wavelet decomposition of Calderón-Zygmund operators on function spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 1 / August 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 29-46
- Print publication:
- August 2004
-
- Article
-
- You have access
- Export citation
The weak-type (1,1) of Fourier integral operators of order –(n–1)/2
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-22
- Print publication:
- February 2004
-
- Article
-
- You have access
- Export citation
The Lp-Lp mapping properties of convolution operators with the affine arclength measure on space curves
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 247-262
- Print publication:
- October 2003
-
- Article
-
- You have access
- Export citation
Spectral theory for random closed sets and estimating the covariance via frequency space
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 603-613
- Print publication:
- September 2003
-
- Article
- Export citation
Two weighted ineqalities for maximal functions related to Cesàro convergence
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 1 / February 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 111-120
- Print publication:
- February 2003
-
- Article
-
- You have access
- Export citation
Analyse conforme sur les algèbres de Jordan
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 2 / October 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 279-300
- Print publication:
- October 2002
-
- Article
-
- You have access
- Export citation
A problem on rough parametric Marcinkiewicz functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 13-22
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation
Calderón-type reproducing formulae on Lipschitz curves and surfaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 33-46
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation
Transference on certain multilinear multiplier operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 1 / February 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 37-55
- Print publication:
- February 2001
-
- Article
-
- You have access
- Export citation
Norm inequalities relating one-sided singular integrals and the one-sided maximal function
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 3 / December 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 403-414
- Print publication:
- December 2000
-
- Article
-
- You have access
- Export citation
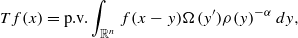
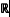 )
)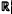
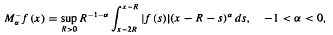 is of weak and restricted weak type (
is of weak and restricted weak type (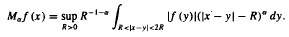 We apply the results to the study of the Cesàro-α convergence of singular integrals.
We apply the results to the study of the Cesàro-α convergence of singular integrals.
 with kernel function Ω in
with kernel function Ω in  +) for 1 < q ≦.
+) for 1 < q ≦.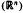
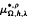 and
and 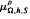 with Ω in
with Ω in 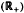
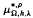 and
and 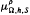 are parametric Marcinkiewicz functions corresponding to the Littlewood-Paley
are parametric Marcinkiewicz functions corresponding to the Littlewood-Paley 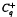 condition, then the
condition, then the 