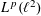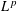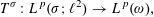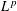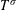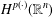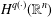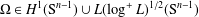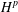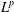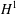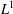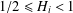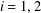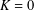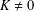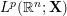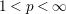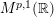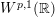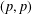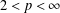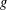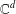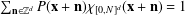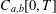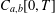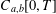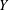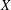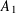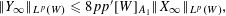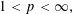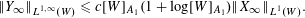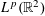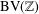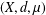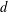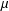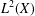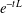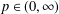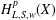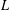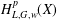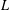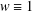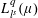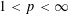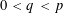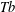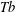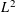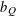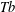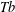Refine listing
Actions for selected content:
271 results in 42Bxx
A TWO-WEIGHT INEQUALITY BETWEEN
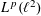 $L^{p}(\ell ^{2})$ AND
$L^{p}(\ell ^{2})$ AND 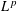 $L^{p}$
$L^{p}$
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 14 February 2018, pp. 284-302
- Print publication:
- 2018
-
- Article
- Export citation
BOUNDEDNESS OF GENERALIZED RIESZ POTENTIALS ON THE VARIABLE HARDY SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 14 August 2017, pp. 255-273
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
A NOTE ON MARCINKIEWICZ INTEGRALS ASSOCIATED TO SURFACES OF REVOLUTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 14 August 2017, pp. 380-402
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
HARDY SPACES ON METRIC MEASURE SPACES WITH GENERALIZED SUB-GAUSSIAN HEAT KERNEL ESTIMATES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 14 August 2017, pp. 162-194
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
ON MULTI-ASSET SPREAD OPTION PRICING IN A WICK–ITÔ–SKOROHOD INTEGRAL FRAMEWORK
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 24 May 2017, pp. 386-396
-
- Article
-
- You have access
- Export citation
SINGULAR INTEGRALS SUPPORTED BY SUBVARIETIES FOR VECTOR-VALUED FUNCTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 231 / September 2018
- Published online by Cambridge University Press:
- 08 May 2017, pp. 101-114
- Print publication:
- September 2018
-
- Article
-
- You have access
- HTML
- Export citation
OPERATING FUNCTIONS ON MODULATION AND WIENER AMALGAM SPACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 17 April 2017, pp. 72-82
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
ON LITTLEWOOD–PALEY FUNCTIONS ASSOCIATED WITH THE DUNKL OPERATOR
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 29 March 2017, pp. 126-138
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
CHARACTERISATIONS OF PARTITION OF UNITIES GENERATED BY ENTIRE FUNCTIONS IN
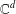 $\mathbb{C}^{d}$
$\mathbb{C}^{d}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 05 January 2017, pp. 281-290
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
A REPRESENTATION FOR THE INVERSE GENERALISED FOURIER–FEYNMAN TRANSFORM VIA CONVOLUTION PRODUCT ON FUNCTION SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 05 January 2017, pp. 424-435
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
TIGHTER BOUNDS FOR THE DISCREPANCY OF BOXESAND POLYTOPES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1091-1113
- Print publication:
- 2017
-
- Article
- Export citation
WEIGHTED INEQUALITIES FOR MARTINGALE TRANSFORMS AND STOCHASTIC INTEGRALS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 20 February 2017, pp. 433-450
- Print publication:
- 2017
-
- Article
- Export citation
HILBERT TRANSFORMS ALONG LIPSCHITZ DIRECTION FIELDS: A LACUNARY MODEL
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 09 February 2017, pp. 351-363
- Print publication:
- 2017
-
- Article
- Export citation
A REMARK ON THE REGULARITY OF THE DISCRETE MAXIMAL OPERATOR
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 01 December 2016, pp. 108-120
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
LITTLEWOOD–PALEY CHARACTERIZATION OF WEIGHTED HARDY SPACES ASSOCIATED WITH OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 10 November 2016, pp. 250-267
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
SHARP INEQUALITIES FOR THE VARIATION OF THE DISCRETE MAXIMAL FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 04 November 2016, pp. 94-107
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
GENERALIZED MORREY SPACES OVER NONHOMOGENEOUS METRIC MEASURE SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 27 October 2016, pp. 268-278
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
TWO-WEIGHT NORM INEQUALITIES FOR VECTOR-VALUED OPERATORS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 26 July 2016, pp. 72-91
- Print publication:
- 2017
-
- Article
- Export citation
GENERALIZED LOCAL
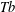 $\mathit{Tb}$ THEOREMS FOR SQUARE FUNCTIONS
$\mathit{Tb}$ THEOREMS FOR SQUARE FUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 25 July 2016, pp. 1-28
- Print publication:
- 2017
-
- Article
- Export citation
Characterizations of bounded mean oscillation through commutators of bilinear singular integral operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 13 July 2016, pp. 1159-1166
- Print publication:
- December 2016
-
- Article
- Export citation