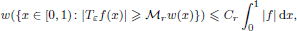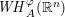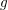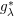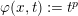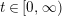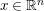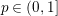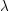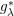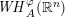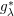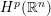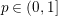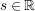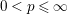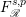Refine listing
Actions for selected content:
271 results in 42Bxx
Sparse Bounds for a Prototypical Singular Radon Transform
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 405-415
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
DICHOTOMY PROPERTY FOR MAXIMAL OPERATORS IN A NONDOUBLING SETTING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 454-466
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
ANALYSIS IN THE MULTI-DIMENSIONAL BALL
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 2 / 2019
- Published online by Cambridge University Press:
- 31 October 2018, pp. 190-212
- Print publication:
- 2019
-
- Article
- Export citation
Pointwise Characterizations of Even Order Sobolev Spaces via Derivatives of Ball Averages
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 15 October 2018, pp. 681-699
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Oscillation and variation for the Riesz transform associated with Bessel operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 18 September 2018, pp. 169-190
- Print publication:
- February 2019
-
- Article
- Export citation
ON THE BILINEAR SQUARE FOURIER MULTIPLIER OPERATORS ASSOCIATED WITH
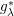 $g_{\unicode[STIX]{x1D706}}^{\ast }$ FUNCTION
$g_{\unicode[STIX]{x1D706}}^{\ast }$ FUNCTION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 28 August 2018, pp. 123-152
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
POINTWISE CONVERGENCE OF SCHRÖDINGER SOLUTIONS AND MULTILINEAR REFINED STRICHARTZ ESTIMATES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 13 August 2018, e14
-
- Article
-
- You have access
- Open access
- Export citation
Improved A1−A∞ and Related Estimates for Commutators of Rough Singular Integrals
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 06 August 2018, pp. 1069-1086
-
- Article
- Export citation
Littlewood–Paley characterizations of fractional Sobolev spaces via averages on balls
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 22 June 2018, pp. 1135-1163
- Print publication:
- December 2018
-
- Article
- Export citation
CONDITIONAL LARGE INITIAL DATA SCATTERING RESULTS FOR THE DIRAC–KLEIN–GORDON SYSTEM
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 21 June 2018, e9
-
- Article
-
- You have access
- Open access
- Export citation
RIESZ TRANSFORMS AND LITTLEWOOD–PALEY SQUARE FUNCTION ASSOCIATED TO SCHRÖDINGER OPERATORS ON NEW WEIGHTED SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 18 June 2018, pp. 201-228
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
Weak-Type Boundedness of the Fourier Transform on Rearrangement Invariant Function Spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 08 June 2018, pp. 879-890
-
- Article
- Export citation
Variable Hardy Spaces Associated with Operators Satisfying Davies–Gaffney Estimates
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 21 May 2018, pp. 759-810
-
- Article
- Export citation
A weighted weak-type bound for Haar multipliers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 22 April 2018, pp. 643-658
- Print publication:
- June 2018
-
- Article
- Export citation
THE HARDY AND HEISENBERG INEQUALITIES IN MORREY SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 480-491
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
FRACTIONAL INTEGRAL OPERATORS ON
 $\unicode[STIX]{x1D6FC}$ -MODULATION SPACES IN THE FULL RANGE
$\unicode[STIX]{x1D6FC}$ -MODULATION SPACES IN THE FULL RANGE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 499-512
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
LITTLEWOOD–PALEY CHARACTERIZATIONSOF ANISOTROPIC WEAK MUSIELAK–ORLICZHARDY SPACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 237 / March 2020
- Published online by Cambridge University Press:
- 16 March 2018, pp. 39-78
- Print publication:
- March 2020
-
- Article
-
- You have access
- HTML
- Export citation
FRACTIONAL FOCK–SOBOLEV SPACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 237 / March 2020
- Published online by Cambridge University Press:
- 06 March 2018, pp. 79-97
- Print publication:
- March 2020
-
- Article
-
- You have access
- HTML
- Export citation
Weighted Vector-Valued Inequalities for a Class of Multilinear Singular Integral Operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 413-436
-
- Article
- Export citation
Local Fractal Interpolation on Unbounded Domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 23 January 2018, pp. 151-167
-
- Article
- Export citation
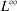
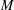
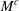
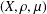
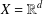
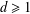
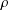
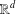
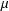
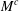
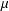
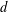
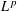
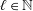
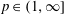
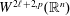
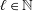
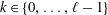
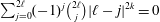
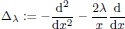
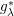

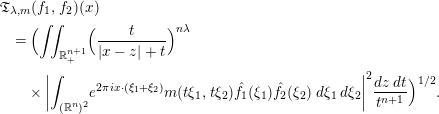
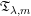
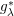
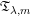
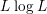
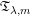
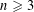
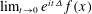
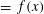
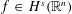
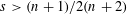
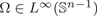
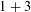
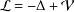
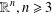
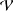
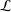
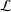
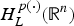
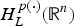
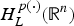
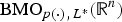
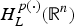
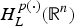
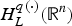
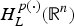
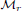 is the
is the