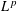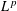Refine listing
Actions for selected content:
271 results in 42Bxx
An almost-periodic solution of Hasegawa–Wakatani equations with vanishing resistivity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 23 June 2016, pp. 983-1003
- Print publication:
- October 2016
-
- Article
- Export citation
SHARP WEIGHTED BOUNDS FOR GEOMETRIC MAXIMAL OPERATORS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 533-547
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
THE
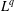 $L^{q}$ ESTIMATES OF RIESZ TRANSFORMS ASSOCIATED TO SCHRÖDINGER OPERATORS
$L^{q}$ ESTIMATES OF RIESZ TRANSFORMS ASSOCIATED TO SCHRÖDINGER OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 25 April 2016, pp. 290-309
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
RIESZ TRANSFORM ESTIMATES IN THE ABSENCE OFA PRESERVATION CONDITION AND APPLICATIONS TO THE DIRICHLET LAPLACIAN
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 08 March 2016, pp. 521-522
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
BOUNDS ON PRICES FOR ASIAN OPTIONS VIAFOURIER METHODS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 57 / Issue 3 / January 2016
- Published online by Cambridge University Press:
- 19 February 2016, pp. 299-318
-
- Article
-
- You have access
- Export citation
UNIONS OF LINES IN
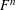 $F^{n}$
$F^{n}$
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 11 April 2016, pp. 738-752
- Print publication:
- 2016
-
- Article
- Export citation
SOME SHARP BILINEAR SPACE–TIME ESTIMATES FOR THE WAVE EQUATION
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 07 March 2016, pp. 719-737
- Print publication:
- 2016
-
- Article
- Export citation
MAXIMAL SEMIGROUP SYMMETRY AND DISCRETE RIESZ TRANSFORMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 14 December 2015, pp. 216-240
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
A NOTE ON THE ENDPOINT REGULARITY OF THE HARDY–LITTLEWOOD MAXIMAL FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 11 December 2015, pp. 121-130
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
DYADIC TRIANGULAR HILBERT TRANSFORM OF TWO GENERAL FUNCTIONS AND ONE NOT TOO GENERAL FUNCTION
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 13 November 2015, e25
-
- Article
-
- You have access
- Open access
- Export citation
HELSON’S PROBLEM FOR SUMS OF A RANDOM MULTIPLICATIVE FUNCTION
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 21 October 2015, pp. 101-110
- Print publication:
- 2016
-
- Article
- Export citation
NONCOMMUTATIVE DE LEEUW THEOREMS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 12 October 2015, e21
-
- Article
-
- You have access
- Open access
- Export citation
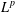 $L^{p}$ BOUNDS FOR NONISOTROPIC MARCINKIEWICZ INTEGRALS ASSOCIATED TO SURFACES
$L^{p}$ BOUNDS FOR NONISOTROPIC MARCINKIEWICZ INTEGRALS ASSOCIATED TO SURFACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 17 August 2015, pp. 380-398
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
QUASI RIESZ TRANSFORMS, HARDY SPACES AND GENERALISED SUB-GAUSSIAN HEAT KERNEL ESTIMATES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 10 August 2015, pp. 508-510
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
ON VECTOR-VALUED TENT SPACES AND HARDY SPACES ASSOCIATED WITH NON-NEGATIVE SELF-ADJOINT OPERATORS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 689-716
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
ON THE WELL-POSEDNESS OF PARABOLIC EQUATIONS OF NAVIER–STOKES TYPE WITH
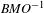 $\mathit{BMO}^{-1}$ DATA
$\mathit{BMO}^{-1}$ DATA
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 5 / November 2017
- Published online by Cambridge University Press:
- 27 April 2015, pp. 947-985
- Print publication:
- November 2017
-
- Article
- Export citation
On the Local Tb Theorem: A Direct Proof under the Duality Assumption
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 13 February 2015, pp. 193-222
-
- Article
- Export citation
MAXIMAL HARDY SPACES ASSOCIATED TO NONNEGATIVE SELF-ADJOINT OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 23 December 2014, pp. 286-302
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
Generalized Morrey Regularity for Parabolic Equations with Discontinuous Data
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 10 December 2014, pp. 199-218
-
- Article
-
- You have access
- Export citation
A SPLITTING PROCEDURE FOR BELLMAN FUNCTIONS AND THE ACTION OF DYADIC MAXIMAL OPERATORS ON
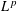 $L^{p}$
$L^{p}$
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 19 November 2014, pp. 199-212
- Print publication:
- January 2015
-
- Article
- Export citation
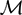
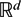
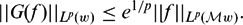
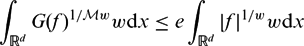
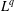
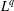
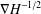
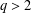
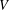
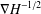
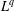
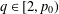
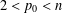
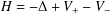
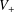
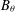
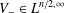
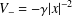

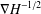
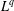
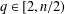
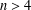
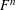
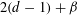
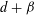
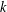
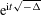
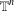
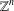

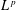

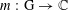
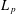
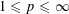
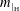
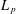
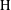
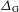
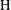
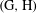
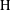
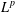
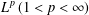
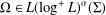
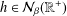
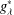
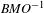
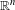
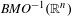
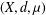
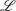
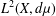
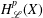
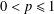
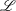
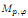 of sublinear operators generated by the parabolic Calderón—Zygmund operator and by the commutator of this operator with bounded mean oscillation (BMO) functions. As a consequence, we obtain a global
of sublinear operators generated by the parabolic Calderón—Zygmund operator and by the commutator of this operator with bounded mean oscillation (BMO) functions. As a consequence, we obtain a global