The covariogram of a compact set A⊂ℝn is the function that to each x∈ℝn associates the volume of A∩(A+x). Recently it has been proved that the covariogram determines any planar convex body, in the class of all convex bodies. We extend the class of sets in which a planar convex body is determined by its covariogram. Moreover, we prove that there is no pair of non-congruent planar polyominoes consisting of less than nine points that have equal discrete covariograms.

Extending previous results of the first author, some new estimates are obtained for maximal operators of Schrödinger type with a complex parameter.

The relation between the fractional integral operator and the fractional maximal operator is investigated in the framework of Morrey spaces. Applications to the Fefferman–Phong and the Olsen inequalities are also included.

We show that if the summability means in the Fourier inversion formula for a tempered distribution f ∈ S′(ℝn) converge to zero pointwise in an open set Ω, and if those means are locally bounded in L1(Ω), then Ω ⊂ ℝn\supp f. We prove this for several summability procedures, in particular for Abel summability, Cesàro summability and Gauss-Weierstrass summability.

We establish the continuity of the Hardy-Littlewood maximal operator on W1,p(Ω), where Ω ⊂ ℝn is an arbitrary subdomain and 1 < p < ∞. Moreover, boundedness and continuity of the same operator is proved on the Triebel-Lizorkin spaces Fps,q (Ω) for 1 < p,q < ∞ and 0 < s < 1.

We study the variance of the fluctuations in the number of lattice points in a ball and in a thin spherical shell of large radius centred at a Diophantine point.

Using the polynomial method of Dvir [On the size of Kakeya sets in finite fields. Preprint], we establish optimal estimates for Kakeya sets and Kakeya maximal functions associated to algebraic varieties W over finite fields F. For instance, given an (n−1)-dimensional projective variety W⊂¶n(F), we establish the Kakeya maximal estimate for all functions f:Fn→R and d≥1, where for each w∈W, the supremum is over all irreducible algebraic curves in Fn of degree at most d that pass through w but do not lie in W, and with Cn,W,d depending only on n,d and the degree of W; the special case when W is the hyperplane at infinity in particular establishes the Kakeya maximal function conjecture in finite fields, which in turn strengthens the results of Dvir.

For a class of convex curves in ℝd we prove that the corresponding maximal operator and Hilbert transform are of weak type Llog L. The point of interest here is that this class admits curves which are infinitely flat at the origin. We also prove an analogous weak type result for a class of nonconvex hypersurfaces.

An important inequality due to Wolff on plate decompositions of cone multipliers is known to have consequences for sharp Lp results on cone multipliers, local smoothing for the wave equation, convolutions with radial kernels, Bergman projections in tubes over cones, averages over finite-type curves in ℝ3 and associated maximal functions. We observe that the range of p in Wolff's inequality, for the conic and the spherical versions, can be improved by using bilinear restriction results. We also use this inequality to give some improved estimates on square functions associated to decompositions of cone multipliers in low dimensions. This gives a new L4 bound for the cone multiplier operator in ℝ3.

We discuss here the boundedness of the fractional integral operator Iα and its generalized version on generalized nonhomogeneous Morrey spaces. To prove the boundedness of Iα, we employ the boundedness of the so-called maximal fractional integral operator Ia,κ*. In addition, we prove an Olsen-type inequality, which is analogous to that in the case of homogeneous type.

We prove sharp estimates for the dilation operator f(x)⟼f(λx), when acting on Wiener amalgam spaces W(Lp,Lq). Scaling arguments are also used to prove the sharpness of the known convolution and pointwise relations for modulation spaces Mp,q, as well as the optimality of an estimate for the Schrödinger propagator on modulation spaces.

We prove certain Lp estimates (1<p<∞) for nonisotropic singular integrals along surfaces of revolution. The singular integrals are defined by rough kernels. As an application we obtain Lp boundedness of the singular integrals under a sharp size condition on their kernels. We also prove a certain estimate for a trigonometric integral, which is useful in studying nonisotropic singular integrals.

We deal with the restriction phenomenon for the Fourier transform. We prove that each of the restriction conjectures for the sphere, the paraboloid and the elliptic hyperboloid in ℝn implies that for the cone in ℝn+1. We also prove a new restriction estimate for any surface in ℝ3 locally isometric to the plane and of finite type.

We study the boundedness properties of Rudin–Forelli-type operators associated to tubular domains over symmetric cones. As an application, we give a characterization of the topological dual space of the weighted Bergman space .

In this paper, we shall give some characterizations of the Hardy space associated with twisted convolution, including Lusin area integral, Littlewood–Paley g-function and heat maximal function.

We use the Freiman theorem in arithmetic combinatorics to show that if the Fourier transform of certain measures satisfies sufficiently bad estimates, then the support of the measure possesses an additive structure. The result is then discussed in light of the Falconer distance problem.

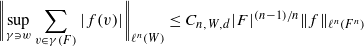
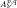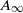Let 𝒳 be a space of homogeneous type in the sense of Coifman and Weiss. In this paper, two weighted estimates related to weights are established for singular integral operators with nonsmooth kernels via a new sharp maximal operator associated with a generalized approximation to the identity. As applications, the weighted Lp(𝒳) and weighted endpoint estimates with general weights are obtained for singular integral operators with nonsmooth kernels, their commutators with BMO (𝒳) functions, and associated maximal operators. Some applications to holomorphic functional calculi of elliptic operators and Schrödinger operators are also presented.

Weconsider the Fourier restriction operators associated to certaindegenerate curves in ℝd for which the highest torsion vanishes. We prove estimates with respect to affine arclength and with respect to the Euclidean arclength measure on the curve. The estimates have certain uniform features, and the affine arclength results cover families of flat curves.

Westudy the boundedness for multilinear fractional integrals on spaces as Morrey spaces and Lipschitz spaces.

Weprove optimal radially weighted L2-norm inequalities for the Fourier extension operator associated to the unit sphere in ℝn. Such inequalities valid at all scales are well understood. The purpose of this short paper is to establish certain more delicate single-scale versions of these.