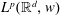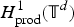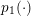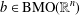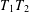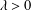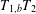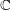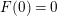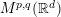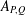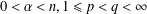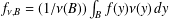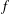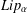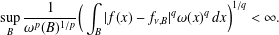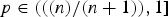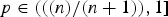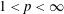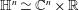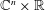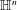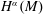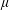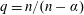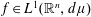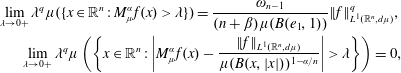Refine listing
Actions for selected content:
271 results in 42Bxx
Weighted estimates for the Calderón commutator
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 23 September 2019, pp. 169-192
-
- Article
- Export citation
Maximal Operator for the Higher Order Calderón Commutator
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 03 September 2019, pp. 1386-1422
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Two boundedness criteria for a class of operators on Musielak–Orlicz Hardy spaces and applications
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 16 July 2019, pp. 13-35
-
- Article
- Export citation
Orlicz–Besov Extension and Imbedding
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 01 July 2019, pp. 222-241
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
A comparison principle for convolution measures with applications
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 28 June 2019, pp. 307-322
- Print publication:
- September 2020
-
- Article
- Export citation
A multiplier inclusion theorem on product domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 20 June 2019, pp. 1073-1088
-
- Article
-
- You have access
- Open access
- Export citation
HERZ–MORREY SPACES ON THE UNIT BALL WITH VARIABLE EXPONENT APPROACHING
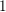 $1$ AND DOUBLE PHASE FUNCTIONALS
$1$ AND DOUBLE PHASE FUNCTIONALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 242 / June 2021
- Published online by Cambridge University Press:
- 13 June 2019, pp. 1-34
- Print publication:
- June 2021
-
- Article
- Export citation
WEIGHTED WEAK TYPE ENDPOINT ESTIMATES FOR THE COMPOSITIONS OF CALDERÓN–ZYGMUND OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 08 April 2019, pp. 320-339
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Muckenhoupt Class Weight Decomposition and BMO Distance to Bounded Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 25 March 2019, pp. 1017-1031
-
- Article
- Export citation
Higher Summability and Discrete Weighted Muckenhoupt and Gehring Type Inequalities
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 11 March 2019, pp. 949-973
-
- Article
- Export citation
COMPOSITION OPERATORS ON WIENER AMALGAM SPACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 08 March 2019, pp. 257-274
- Print publication:
- December 2020
-
- Article
-
- You have access
- HTML
- Export citation
CHARACTERIZATIONS OF BMO AND LIPSCHITZ SPACES IN TERMS OF
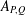 $A_{P,Q}$ WEIGHTS AND THEIR APPLICATIONS
$A_{P,Q}$ WEIGHTS AND THEIR APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 381-391
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Hausdorff operators on holomorphic Hardy spaces and applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1095-1112
- Print publication:
- June 2020
-
- Article
- Export citation
Explicit Salem sets, Fourier restriction, and metric Diophantine approximation in the p-adic numbers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1265-1288
- Print publication:
- June 2020
-
- Article
- Export citation
Variational characterization of Hp
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 15 January 2019, pp. 1123-1134
- Print publication:
- October 2019
-
- Article
- Export citation
Compactness of Commutators of One-Sided Singular Integrals in Weighted Lebesgue Spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 10 January 2019, pp. 655-665
-
- Article
- Export citation
Discrete Multilinear Spherical Averages
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 243-246
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Marcinkiewicz Multipliers and Lipschitz Spaces on Heisenberg Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 607-627
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Pointwise Convergence of Solutions to the Schrödinger Equation on Manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 983-995
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
On the Limiting Weak-type Behaviors for Maximal Operators Associated with Power Weighted Measure
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 313-326
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation