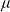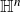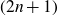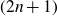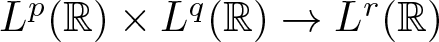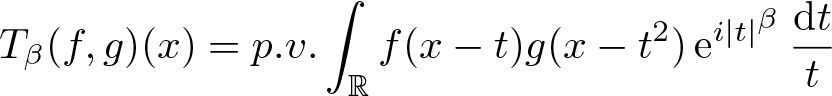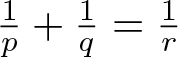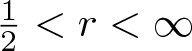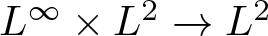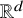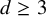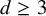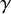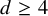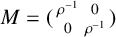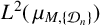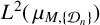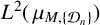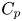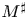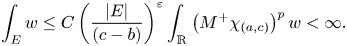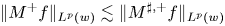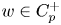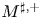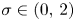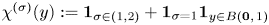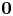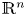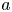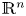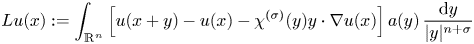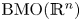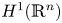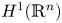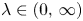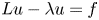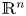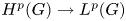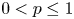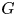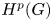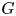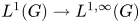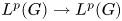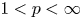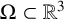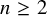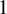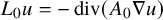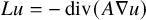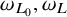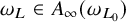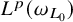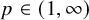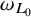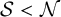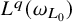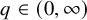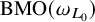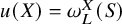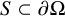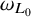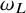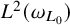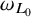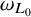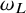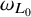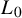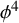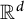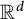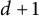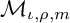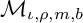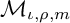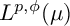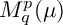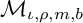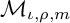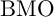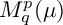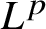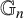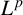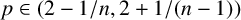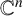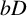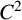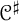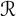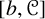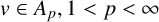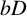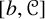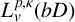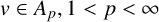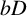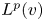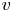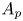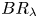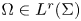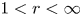Refine listing
Actions for selected content:
271 results in 42Bxx
Necessary condition for the L2 boundedness of the Riesz transform on Heisenberg groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 23 May 2023, pp. 445-458
- Print publication:
- September 2023
-
- Article
- Export citation
The boundedness of the bilinear oscillatory integral along a parabola
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 03 April 2023, pp. 54-88
-
- Article
- Export citation
Sharp smoothing properties of averages over curves
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 10 February 2023, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NONSPECTRAL PROBLEM FOR PLANAR MORAN–SIERPINSKI MEASURES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 11 January 2023, pp. 308-319
- Print publication:
- October 2023
-
- Article
- Export citation
One-sided $C_{p}$
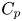 estimates via $M^{\sharp }$
estimates via $M^{\sharp }$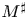 function
function
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 27 December 2022, pp. 2079-2105
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On BMO and Hardy regularity estimates for a class of non-local elliptic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 14 December 2022, pp. 2025-2052
- Print publication:
- December 2023
-
- Article
- Export citation
Fourier multipliers for Hardy spaces on graded Lie groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 02 November 2022, pp. 1729-1750
- Print publication:
- October 2023
-
- Article
- Export citation
Divergence of mock Fourier series for spectral measures
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 17 October 2022, pp. 1818-1832
- Print publication:
- December 2023
-
- Article
- Export citation
Polynomial null solutions to bosonic Laplacians, bosonic Bergman and Hardy spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 13 October 2022, pp. 958-989
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
STRICHARTZ ESTIMATES FOR THE WAVE EQUATION INSIDE CYLINDRICAL CONVEX DOMAINS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 08 August 2022, pp. 304-312
- Print publication:
- April 2023
-
- Article
- Export citation
On the
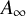 $A_{\infty }$ condition for elliptic operators in 1-sided nontangentially accessible domains satisfying the capacity density condition
$A_{\infty }$ condition for elliptic operators in 1-sided nontangentially accessible domains satisfying the capacity density condition
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 05 August 2022, e59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quadratic Klein-Gordon equations with a potential in one dimension
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 11 July 2022, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the general dyadic grids on
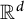 ${\mathbb {R}}^d$
${\mathbb {R}}^d$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 08 July 2022, pp. 1147-1175
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FRACTIONAL TYPE MARCINKIEWICZ INTEGRAL AND ITS COMMUTATOR ON NONHOMOGENEOUS SPACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 03 June 2022, pp. 801-822
- Print publication:
- December 2022
-
- Article
- Export citation
Bounds for spectral projectors on tori
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 12 May 2022, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global Strichartz estimates for the Dirac equation on symmetric spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 12 May 2022, e25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $\boldsymbol {L^{p}}$ REGULARITY OF THE SZEGÖ PROJECTION ON THE SYMMETRISED POLYDISC
$\boldsymbol {L^{p}}$ REGULARITY OF THE SZEGÖ PROJECTION ON THE SYMMETRISED POLYDISC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 12 May 2022, pp. 481-490
- Print publication:
- December 2022
-
- Article
- Export citation
ON THE INHOMOGENEOUS VINOGRADOV SYSTEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 19 April 2022, pp. 396-403
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOUNDEDNESS AND COMPACTNESS OF CAUCHY-TYPE INTEGRAL COMMUTATOR ON WEIGHTED MORREY SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 08 March 2022, pp. 36-56
- Print publication:
- August 2022
-
- Article
- Export citation
Weighted estimates for Bochner–Riesz operators on Lorentz spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 28 February 2022, pp. 654-678
- Print publication:
- April 2023
-
- Article
- Export citation