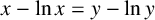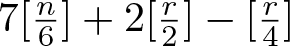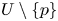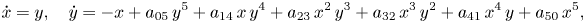Refine listing
Actions for selected content:
112 results in 34Cxx
Limit cycles near a nilpotent center and a homoclinic loop to a nilpotent singularity of Hamiltonian systems
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 October 2025, pp. 1-36
-
- Article
- Export citation
The dichotomy spectrum approach for a global nonuniform asymptotic stability problem: Triangular case via uniformization
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 12 September 2025, pp. 1-29
-
- Article
- Export citation
Well-posedness and averaging principle for non-Gaussian McKean–Vlasov stochastic differential equations with locally Lipschitz coefficients
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-44
-
- Article
- Export citation
Atypical bifurcation for periodic solutions of ϕ-Laplacian systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 03 September 2025, pp. 1-27
-
- Article
- Export citation
Evans function, parity and nonautonomous bifurcations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 August 2025, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BIFURCATION ANALYSIS AND FAST APPROACH OF A LESLIE-TYPE PREY–PREDATOR MODEL INVOLVING ALLEE EFFECT
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 22 August 2025, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MULTIPLE LOCAL AND GLOBAL BIFURCATIONS AND THEIR ROLE IN QUORUM SENSING DYNAMICS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 09 April 2025, e17
-
- Article
- Export citation
GENERIC PLANAR PHASE RESETTING NEAR A PHASELESS POINT
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 08 April 2025, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ANALYTICAL APPROXIMATIONS OF LOTKA–VOLTERRA INTEGRALS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 02 April 2025, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global dynamics of 3D type-K monotone Lotka–Volterra system with the identical intrinsic growth rate
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 31 January 2025, pp. 1-54
-
- Article
- Export citation
Continuum limit for interacting systems on adaptive networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 06 December 2024, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integrability of special quadratic systems with invariant hyperbolas
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1-27
-
- Article
- Export citation
General study on limit cycle bifurcation near a double eight figure loop
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 November 2024, pp. 1-17
-
- Article
- Export citation
A diffusive plant-sulphide model: spatio-temporal dynamics contrast between discrete and distributed delay
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 28 October 2024, pp. 811-828
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Binary pattern retrieval with Kuramoto-type oscillators via a least orthogonal lift of three patterns
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 16 May 2024, pp. 448-463
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Emergent behaviours of a non-abelian quantum synchronisation model over the unitary group
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 30 April 2024, pp. 328-348
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global centres in a class of quintic polynomial differential systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-16
-
- Article
- Export citation
Limit cycles in a rotated family of generalized Liénard systems allowing for finitely many switching lines
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 21 March 2024, pp. 2121-2149
- Print publication:
- December 2025
-
- Article
- Export citation
Bifurcations and pattern formation in a host–parasitoid model with nonlocal effect
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1855-1894
- Print publication:
- October 2025
-
- Article
- Export citation
Continuous dependence of stationary distributions on parameters for stochastic predator–prey models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 22 February 2024, pp. 1010-1028
- Print publication:
- September 2024
-
- Article
- Export citation